数検1級と検索をかけてホームページに訪れていただける方が多いようで嬉しく思います。大人の方や受験を終えた高校生、そして4月から数学を頑張るぞ!と燃えている人などいらっしゃるかと思います。
-

-
【数学検定1級】参考書の順番で合格率が上昇(過去問は難易度に注意!)
続きを見る
特に、数検1級の出題範囲の高校数学範囲を絶対に得点源にしたい!という方をターゲットとして受験数学界の大御所『大学への数学』の正しい使い方を紹介して行きます。もちろん、数学が苦手な方のために様々なレベルの方を意識した記事にしたいと考えています。
-

-
大学受験数学の攻略法!教科書からでも最難関までOK
続きを見る
月刊『大学への数学』の立ち位置
東京出版が出版されている数学関係の書物の中で、大学受験の範囲を意識した教材は2種類あります。
- 1つは受験数学では避けては通れないシリーズ『1対1対応の演習』などの増刊号であり、
- 2つは本記事でメインの月刊『大学への数学』という雑誌になります。
-

-
大学受験数学の攻略法!教科書からでも最難関までOK
続きを見る

しかし、月刊『大学への数学』などの月刊誌はレベルの統一がなく、1冊の号の中に複数のレベルの記事が存在している状態なのです。
そのため、学習の初心者の方が挑戦しようとしても正しい使い方を知らないために、挫折をするか、誤った使い方をしてしまい実力が付いていると勘違いしてしまう状況が起こり得るのです。
そのため、学習者としての我々がすべきことは月刊『大学への数学』のしっかりといた立ち位置を把握することなのです。
数学検定としての立ち位置
難易度の比較を行うと、数検1級>月刊『大学への数学』>数検準1級となります。
しかし、数検1級の高校範囲に限定をするならば、
月刊『大学への数学』>数検1級の高校範囲>数検準1級(満点レベル)となるでしょう。
なぜそのようになるのかの根拠がしっかりとあります。それは受験数学の立ち位置を考えれば判明します。
受験数学としての立ち位置
まず、受験数学の参考書の最難関の本はこちらになります。
正直に申し上げますと、本書の難易度はとち狂っていると思います笑
1冊の参考書で数検1級の高校範囲をコテンパンにしてやりたい!という方以外は下手に手を出す代物ではないと思います。
数検1級がどのくらい恐ろしいかはこちらをご覧ください。
-

-
【数学検定1級】参考書の順番で合格率が上昇(過去問は難易度に注意!)
続きを見る
ちなみに、京大の数学特別入試などの対策など、受験数学の現実的な最高難度の参考書はこちらです。
知り合いでこれと格闘している人がいますが滅茶苦茶に数学得意な人です。高校生でこれをやっていたらかなりの変態です。本書は月刊『大学への数学』で難易度Dレベルに近い問題が沢山並んでいる本です。
ここで難易度というワードが出てきましたね。説明します。
月刊『大学への数学』では、受験数学の難易度を1から10に分けて各問題ごとに難易度を数字で表現しています。
- ランクAが1〜5
- ランクBが6〜7
- ランクCが8〜9
- ランクDが10
となっています。具体例が下のようになります。

なんだか変な米みたいな記号ありますね。これは入試本番でその問題にかけられる理想的な解答時間です。
- 米が10分
- ○が5分
となっております。このように問題ごとに難易度と目標解答時間が与えられている点はかなり高評価に値すると思います。
以上を考慮すると、月刊『大学への数学』は教科書の例題レベル〜最難関大学で合否を分ける問題を攻略するためのコスパ最高の本であると言えるでしょう。
そのため、当然数検準1級のレベルは軽く凌駕しています。
月刊『大学への数学』4月号〜3月号までの紹介
僕は2002年〜2018年度の月刊『大学への数学』を持っています。
さらに詳しく書きますと、2010年4月号〜2019年3月号までは今手元にあるとことです。
それよりも古い年度となりますと、抜けている号がチラホラある感じになります。
その内容にザッと目を通したところ僕は2つの事実に気づきました。
- 年度が違っていても掲載されている内容は問題を含めてほぼ同一
- 使用者のレベルによって使い方が異なる
ほぼ同一とは、全く同じ問題ではないが、その問題を解くために使う知識や解くためのストーリーがほとんど同じであるという意味です。
数学が苦手な人はそこの所を理解してくれないイメージがあります。

使用者のレベルによる注意点は次の章に回すといて本章では、各号に掲載されている出題分野を全部提示して行こうと思います。
解説の順番は各号のページの若い順から追っていきますね!
月刊『大学への数学』4月号
月刊『大学への数学』4月号では、数学ⅠAⅡB範囲の超頻出問題がAレベル中心の問題セットとBレベル中心の問題セット、計2セットが15問±2題で掲載されております。例えばこのような感じにです。

対して、解答はこのような体裁で紹介されています。無駄が一切ない美しい解答です。

ちなみに本問はBランクです。目標解答時間は25分と書いています。これをキツイと思うかは人それぞれだと思います。しかし、個人的には本番を想定した絶妙な難易度設定&時間設定だと確信しています。
また、本問は早稲田の問題ですが、解答の後のコラムなどに早稲田の数学は簡単な年と難しい年の差が激しいなどと受験上有益なコメントもありますので、購入して損なしです。
次に、数学ⅠまたはⅡ相当の式と計算の分野がAレベル中心の問題セットとA〜Cレベルの問題セット、計2セット15問±2題掲載されております。

このような問題です。雑誌を確認したところ、難易度はBで制限時間は20分でした。数検では準1級の2次試験レベルですね。と言った具合に分析が可能です。
さらに、4月号は東京大学などの主要大学の問題と解答が掲載されています。具体的なリストを次に載せますね!
- 慶大・理工
- 同大・理系
- 慈恵医大
- 早大・理工系
- 東大
- 東工大
- 名大
- 京大
- 阪大
さらに来年度の予想が書いてあったりもします。
ここの部分を見るために月刊『大学への数学』を購入する知り合いがいるほど、お宝情報が掲載されているわけですね。オススメ!
大学への数学 2018年 04月号 雑誌 /東京出版(渋谷区)
最後には日本数学オリンピック本選の問題が掲載されています。参考までに。
月刊『大学への数学』5月号
月刊『大学への数学』5月号では、数Ⅱの微積分がAレベル中心の問題セットとBレベルの問題セット、計2セット15問±2題掲載されております。

やはり月刊『大学への数学』の凄いなと思うところは、やはり掲載問題が次の年度の予想問題となっているところですよ。数学が得意な方はわかると思いますが、本問は頻出問題ですよね。
個々のパターンは『1対1対応の演習』にあり、それを組み合わせて行くだけですから。
次に、数学Ⅰの二次関数の分野がAレベル中心の問題セットとA〜Cレベルの問題セット、計2セット10問±2題掲載されております。

例えば、このような問題です。こう言った分野は二次関数を一通り勉強した高校1年生の方なんかは相性が良いのではないでしょうか?
そして、月刊『大学への数学』5月号は4月号に続いて次の大学入試問題の問題と解説があります。
4月号と比べてより大学のバリエーションが広がっているのがわかりますね。
- 北大・理系
- 東北大・理系
- 一橋大
- 医科歯科大
- 新潟大・理系
- 金沢大・理系
- 神戸大・理系
- 広大・理系
- 九大・理系
- 慶大・医
ラスボスがきちんとラスボスしているのが5月号の特徴です笑
大学への数学 2018年 05月号 雑誌 /東京出版(渋谷区)
5月号には数学オリンピック関連の話題はありません。
月刊『大学への数学』6月号
月刊『大学への数学』6月号の目玉は数学Bのベクトルです。Aレベル中心の問題セットとBレベルの問題セット、B〜Cレベルのセット計3セットが15問±2題掲載されております。ちなみにベクトルのCレベルは次のような問題です。

レベルとしては『やさしい理系数学』を終えていれば対処可能ですが、いかがでしょうか??
このように月刊『大学への数学』6月号はベクトルの問題を50問以上に触れられますので、入試でベクトルが大問1問分になる大学を受験する方にとっては有益な情報源となるはずです。

次に、数学ⅠとⅡの方程式という分野では、Aレベル中心の問題セットとBレベルの問題セットの計2セットが15問±2題掲載されております。ここでは次のような意表をつかせる問題も掲載されている点が特徴です。
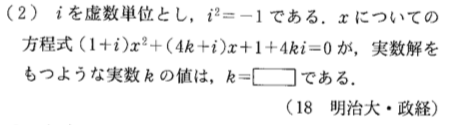
この問題で解の公式を使ってしまったらさいならーですからね!
そして6月号からは数学Ⅲの記事も入ってきます。今月号は極限です。極限って適当に理解している人が多いと思いますが、この号を見ていただければ「あ、俺(私)って適当にリミットしてたわ・・・」と猛省するはずです。
さて、本分野はAレベル中心の問題セットとA〜Cレベルの問題セットの計2セットが15問±2題掲載されております。Aレベルのまとめ問題が定期試験などでめっちゃやくに立つと思いますので参考にしてください。難しい方のセットでは難関大〜最難関大が好んで出題してくるパターンに分けた問題の整理・解説をしてくれているという神具合ですよ。

THEテンプレ問題乙!(シュタゲのダルの真似)って思った方はかなりの腕前ですよ?!
この高コスパの6月号は下記からご閲覧ください!
大学への数学 2018年 06月号 雑誌 /東京出版(渋谷区)
月刊『大学への数学』7月号
月刊『大学への数学』7月号では、受験数学最難関分野の1つである通過領域の問題との戦いになります。
分野では数学Ⅱの図形と方程式になります。Aレベル中心の問題セットとBレベルの問題セット、B〜Cレベルのセット計3セットが15問±2題掲載されております。
良くもまあ毎年似たような問題を大学は出題しているなーと思ってしまうほど問題が類似しています笑

だいたいこれでランクBです。Cじゃないか!と思った方はまだまだ修行が足りません(辛口)通過領域はそれほどに難しい分野なのです。
もっと言うと存在と言う言葉にどれくらい親しんでいるか?で勝負が決まる分野だと思って間違いないと思います。
しかし悲しいかな、数検1級では全然出ません!やはり東大をはじめとする大学入試特有の難しさなのでしょうね。
次に、数学ⅠとⅡの範囲では、不等式がきます。Aレベル中心の問題セットとB〜Cレベルの問題セットの計2セットが15問±2題掲載されております。ここはたまに難問が紛れ込んでおりますのでマニアの方にとってはたまらないでしょうね笑
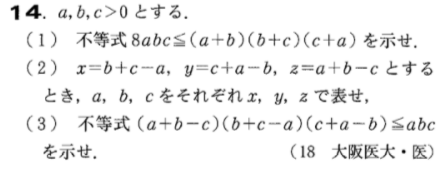
このように単科医科大学などの特殊な数学の試験をしてくる大学の対策に有益なページです。ちなみに本問は納得のCランク!クラシカルな良問ですね。
数学Ⅲの分野では微分法が掲載されています。Aレベル中心の問題セットとB〜Cレベルのセット計2セットが15問±2題掲載されております。ここでも私立医学部の一問一答式の問題などが掲載されていて教材としての質を高めているように感じます。
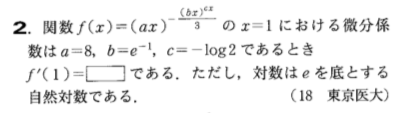
特に今月号の目玉は通過領域に尽きます。東大を目指す方は購入しといて間違いないです。
大学への数学 2018年 07月号 雑誌 /東京出版(渋谷区)
月刊『大学への数学』8月号
月刊『大学への数学』8月号では、数学Bの数列がメイン記事になります。Aレベル中心の問題セットとBレベルの問題セット、B〜Cレベルのセット計3セットが15問±2題掲載されております。今月号は特に問題のバリエーションが多く何を掲載するば良いか迷うほどです。
次に、数学Ⅱの分野では、指数関数・対数関数・三角関数が掲載されております。Aレベル中心の問題セットとBレベルの問題セット計2セットが15問±2題掲載されております。

しっかりと絶妙な問題を持ってくるセンスに脱帽です。本問はBランクの解答時間30分!他の号の特集記事と比べて難易度が低い点が特徴です。
なぜなら、この指数関数・対数関数・三角関数は数学Ⅲまで考えた時に、ただの道具に成り果てるからです。
この分野はただの計算ドリルに過ぎないと言う意識を持っていただければ嬉しいです。
数検準1級の難易度にドンピシャです!数検1級にもぼちぼち役立ちます。
そして数学Ⅲでは積分の計算が載っています。Aレベル中心の問題セットとBレベルの問題セット計2セットが15問±2題掲載されております。積分はまず計算に慣れることから大変なのでこのチョイスには僕は大賛成です!
積分の計算能力に自身がないって方は是非とも8月号を全力でススメます!数検1級にも類題の出題歴あり。
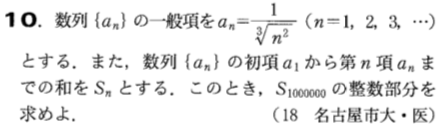
阪大では4万でしたね。(←わかる人にはわかる?)このように絶対にコレ合否分けたでしょう?って問題がズラリ!その壮観さにしびれます。
大学への数学 2018年 08月号 雑誌 /東京出版(渋谷区)
月刊『大学への数学』9月号
月刊『大学への数学』9月号では、受験数学最難関分野の一角である整数問題との戦いがメインになります。Aレベル中心の問題セットとBレベルの問題セット、B〜Cレベルのセット計3セットが15問±2題掲載されております。

あっ・・・。
と言う問題もあれば、

テンプレから外れてしまって泣いている問題も逃さずに掲載しています笑
整数問題はその解法の多さと見抜きにくさで難問率NO1の分野です。ですから、この分野は唯一毎年問題が被ることが少ない分野です。深追いは禁物です。数検1級を目指す方は2次試験で必ず整数問題が出るので購入しない手はないでしょう笑
大学への数学 2018年 09月号 雑誌 /東京出版(渋谷区)
ヤギもこちらを見ています!
次に、数学Ⅰの分野では三角比がテーマとなります。Aレベル中心の問題セットとBレベルの問題セット計2セットが15問±2題掲載されております。北大・理系などを受験する方は是非とも要チェックのページです。

パッと見、方針をどのように選択するか?と迷う問題が多いので、図形問題で解法の閃きスピードを強化したい人に特にオススメです。
数学Ⅲ範囲では、積分の面積がテーマとなります。Aレベル中心の問題セットとBレベルの問題セット計2セットが15問±2題掲載されております。ここは東工大や東大レベルの問題がそびえ立ちます。

本問は簡単な問題ですが、本ページは問題のレベル差が大きい(計算量の違い)のでその点にはご注意を。
月刊『大学への数学』10月号
月刊『大学への数学』10月号では、個人的に一番面倒くさい号です笑
なぜなら場合の数のメイン回だからです。Aレベル中心の問題セットとBレベルの問題セット、B〜Cレベルのセット計3セットが15問±2題掲載されております。問題もタラタラ長いのでサンプル問題の掲載は見送らせていただきます。個人的にはここをやり込んでもあまり点数アップは見込めないと思います。深みにハマり過ぎないようにご注意を。
個人的には本分野を難しくしている理由が、数え上げと言う整数が持つ性質を全面に押し出しているからであると思っています。整数が潜むために難しいわけですね。
次に、数学Aの集合が来ます!また面倒くさい分野が来ました・・・。しかもやり込んでも・・・略

センター試験として見ても若干のオーバーワーク気味を感じますし、やはり僕と10月号は相性合わないですね。
そして極め付けは数学Ⅲの体積(受験数学最難関分野の1つ)・弧長です。どこまで10月号は読者に刃を差しむけるのでしょう!

体積ってテンプルだってわかっても計算が追いつかなければ丸がもらえないですから大変ですよね。数検1級との相性は最高です。
そんな10月号も見てやってください。
大学への数学 2018年 10月号 雑誌 /東京出版(渋谷区)
月刊『大学への数学』11月号
月刊『大学への数学』11月号では、東大・一橋で点の取り所の確率がメインになります。Aレベル中心の問題セットとBレベルの問題セット、B〜Cレベルのセット計3セットが15問±2題掲載されております。10月号と違って僕は大好きな号です。
確率は数え上げのタイプと確率漸化式タイプを上手く織り込んで隠してあり、読者がどっちを使うのかな???と判断させる構成のため、とっても力がつくと思います。サンプル問題は内緒です。開いて問題を見たときの感動を味わって見てください。
大学への数学 2018年 11月号 雑誌 /東京出版(渋谷区)
数学Ⅲでは複素数平面の特訓が待ち受けます。Aレベル中心の問題セットとBレベルの問題セット、B〜Cレベルのセット計3セットが15問±2題掲載されております。最近、東大では複素数平面が熱いですよね。他の大学もちょこちょこ難易度が上昇している感じがあるので、是非、次の点を意識して実力をあげて下さい。
複素数を3つの方法で見る目を養おう。数そのものとして、回転相似変換の関数として、ベクトルとして

最難関大学レベルの問題ですが、意外にいけませんか?
複素数平面は努力すればするほど完答率があがる分野ですので根気が必要です。頑張って下さいね。
月刊『大学への数学』12月号
月刊『大学への数学』12月号からは2月号までは総合演習になります。今月は数式の演習です。全部で50問は超える分量です。
また11月号までと比較をするとやはり難易度は上昇しています。つまり、数学の実力者は12月号〜2月号までを購入するのが上手いやり方な訳ですね!
大学への数学 2018年 12月号 雑誌 /東京出版(渋谷区)
大学への数学 2019年 01月号 雑誌 /東京出版(渋谷区)
大学への数学 2019年 02月号 雑誌 /東京出版(渋谷区)

一見簡単そうですが・・・。
さて、数学Ⅲでは二次曲線がメインとなります。Aレベル中心の問題セットとBレベルの問題セット計2セットが15問±2題掲載されております。

お分かりのように、二次曲線の分野ですが、普通に微積と融合されています。その他には二次曲線の性質を証明させる問題など、嫌な問題もしっかりと掲載されている点から僕は、月刊『大学への数学』から逃げない姿勢を感じます。並大抵の編集力ではこなせないでしょうね。中の人お疲れ様です。
月刊『大学への数学』1月号
月刊『大学への数学』1月号では、図形の融合問題がメインになります。12月号より難しいのが実情です。これはねぇー東大志望者は絶対に買ったほうが良いと思うんです。

このようにテンプレから外れて来ている問題が多いのが1月号の特徴です。テンプレから外れれば外れるほど受験数学の難易度は上昇するので周りの受験生にも差をつけることが可能です。しかし数検1級対策を考えると1月号を購入する選択はちょっとずれてるかなーと感じます。
そして1月号には防衛医科大学校の問題が載っています。Dランク問題が紛れ込んでいる可能性大なので面白いですよ!しかし癖がある問題もある学校のため、問題を解く際にはよく吟味してからの方が良いでしょうね。
月刊『大学への数学』2月号
月刊『大学への数学』2月号では、THE・融合問題しか載っていません笑

問題文が長過ぎて見切れてしまうほどの問題たちがあなたを待ち受けます。2月号は僕の中ではやり過ぎな号です。
つまり月刊『大学への数学』の中で最も難易度が高い号が2月号になるわけです。
しかも数検1級の1次試験(2次ではない!)と類似問題が多々見受けられるので、数検1級チャレンジャーの方は是非とも購入すべきです。
2月号のラスボスは京都大く・理学部(特色入試)の問題と解説です。レベル高過ぎです。東大前期を志望する方は読まなくて全然OKです。ただし数検1級チャレンジャーは2次試験の思考力養成のためにウンウン考ええて損はない素晴らしい問題達です。例えるならばラスボスの間に行くまでの敵との戦闘というイメージですかね。
月刊『大学への数学』3月号
月刊『大学への数学』3月号では、1年間お疲れさま!な号です笑
以前は自治医科大学の過去問集などが掲載されていましたが現在はないようです。
代わりに早期に行われた医系の大学入試問題が掲載されています。
- 日本医大
- 順天堂大・医
- 立命館大・理系・・・
- センター試験
最後で興ざめですかね?笑
とにかく2月号との落差がすごいので2月号の難易度を期待して3月号を購入してしまうとがっかりするかも???
でも、しれっと日本数学オリンピック予選のコーナーがありますのでよろしく!
医系を目指す方にとってはバイブルな3月号はこちらからどうぞ。
大学への数学 2019年 03月号 雑誌 /東京出版(渋谷区)
高校数学の分野別の内容が何月号にあるのか?
では、今度は先に勉強したい分野があって、それは何月号か?について紹介します。
数学Ⅰ
数と式:4月号
二次関数:5月号
三角比:9月号
数学A
場合の数:10月号
確率:11月号
整数:9月号
数学Ⅱ
方程式:6月号
不等式:7月号
図形と方程式:7月号
三角関数:8月号
指数関数・対数関数:8月号
微分積分:5月号
数学B
ベクトル:6月号
数列:8月号
数学Ⅲ
二次曲線:12月号
極限:6月号
微分:7月号
積分の計算:8月号
積分の面積:9月号
積分の体積と弧長:10月号
融合問題(数式)
12月号
融合問題(図形)
1月号
融合問題
2月号
大学入試問題
4月号
- 慶大・理工
- 同大・理系
- 慈恵医大
- 早大・理工系
- 東大
- 東工大
- 名大
- 京大
- 阪大
5月号
- 北大・理系
- 東北大・理系
- 一橋大
- 医科歯科大
- 新潟大・理系
- 金沢大・理系
- 神戸大・理系
- 広大・理系
- 九大・理系
- 慶大・医
3月号
- 日本医大
- 順天堂大・医
- 立命館大・理系・・・
- センター試験
数学オリンピック予選
3月号
数学オリンピック本選
4月号
学習者のレベルを考慮した学習法の提示
本記事で月刊『大学への数学』の様子はご理解いただけましたでしょうか?本格的な本であると思っていただければOKです。では、最後にあなたのレベルに応じた使用法を提案させていただきます。
教科書レベルで精一杯
Aレベルの記事を徹底的にやりこむことをオススメします。その時点で『1対1対応の演習』に手が届く実力が養成されます。すなわち受験数学の入り口に立てる学力になります。
『1対1対応の演習』の例題は解けるが・・・
上述の方はかなり多いと多います。そのような方はBランクの記事をやり込んで下さい。『1対1対応の演習』の何倍も良い効率的な学習が可能となるでしょう。この時点で模擬試験の偏差値でインフレを起こす準備が整ったと言って差し支えないと思います。
冠模試でA判定を取りたい!
そのような方はDランクを除く全ての問題にトライしてみて結果を待ちましょう。実際に本書を隅から隅まで使用している方って化け物並の数学力のはずですので。
そしてラスボスへ
1年分を回せた方は数検1級に挑んでも0点は防げるはずです。数検1級との戦いを楽しんで数学の楽しみを再発見されることを願っております。
果てには東大院試の突破も見えてくると思うので、志望者の方は下記記事を参考に頑張って下さいね!
最後に1年分の月刊『大学への数学』をまとめて終わらせていただいます。お読みいただき、ありがとうございます。
















