連立方程式と聞いて、何をあなたは思いますか?
- 数学が超得意な人→線形代数で出てくるやつじゃん!(数検1級レベルです)
- 数学が得意な人→鶴亀算を方程式で解くやつでしょ?
- 数学が苦手な人→式変形がわかんないやつだ!
数学が苦手な人などの意見を持ち出しましたが、大方このようなイメージでしょうね。
僕が中学生の頃は、「2直線の共有点を求める問題で使う」など、視覚化まで考えを深められた人って少なかったです。
おそらく、中学校では浅い理解のまま連立方程式の学習が進んでしまう生徒が多いのでは?
と思い、深い理解そして今後の大学受験の数学などに向けてしっかりとした土台を作っていただくべく、連立方程式関連のお話をさせていただきます。
この記事は数検4級レベルが中心です!
内容理解へのスムーズさを優先するので、連立不等式という数検準2級レベル(高1範囲)のお話が出てきますが、頑張りましょう!
連立方程式の利用という場面は日常にあふれています
鶴亀算という算数を勉強した人は多いでしょうね。
あれが算数らしい算数だと僕は思うんです。
- 鶴亀算は2つのわからないモノを面積図を書いて出します。
- 数学では2つのわからないモノを方程式で解きます。


面積図に頼ることの欠点
- 3つの未知数(変数)が登場した時に手に負えなくなる
- 2つの変数の問題でも複雑になったら手に負えなくなる
算数の欠点そのものですよね。
対して連立方程式を用いるメリットは底知れません!
連立方程式を使う代表的なメリット
- 変数が2個より多くても必ず問題は解ける!(大学1年レベルのもある!)
- 問題が複雑になっても立式さえできれば本質的にはおしまい!
だからこそ、僕たちは連立方程式を学ぶのです!
連立方程式を解く手順
例えば次のような問題があります。
ある人が林檎(りんご)と蜜柑(みかん)を買いました。合わせて5個です。
林檎1個は50円で蜜柑1個は100円で、合計金額は400円でした。
林檎と蜜柑のそれぞれの個数を求めよ。
もちろん面積図は禁止です笑
こういう算数にずっとこだわる人ほど数学が苦手になる法則ってあります→こちら
さて、ではどのように考えていくのでしょうか?
どのような問題が来ても次の3ステップで問題は解決します。
連立方程式の3ステップ
- 変数\(x\)と\(y\)を決める
- 方程式を作る(変数が2個なら2つの方程式は必要!)
- 連立方程式を解いて変数\(x\)と\(y\)を求める。
では順に追っていきましょう。
変数\(x\)と\(y\)をそれぞれ、林檎の個数、蜜柑の個数とする。
すると、個数の関係と金額の関係から次の連立方程式が立式できる。
\(\begin{eqnarray} \left\{ \begin{array}{l} x + y = 5 \\ 50x + 100y = 400 \end{array} \right. \end{eqnarray}\)
なるほど。では、2つの式から\(x\)と\(y\)を何とかして求めましょう!


消去法で解く
\(\begin{eqnarray} \left\{ \begin{array}{l} x + y = 5 \\ 50x + 100y = 400 \end{array} \right. \end{eqnarray}\)
上の式の両辺を50倍すると、次のようになる。
\(\begin{eqnarray} \left\{ \begin{array}{l} 50x + 50y = 250 \\ 50x + 100y = 400 \end{array} \right. \end{eqnarray}\)
そうすると、下の式から上の式を引いて、\(50y=150\)になり、\(y=3\)となる。
それを\(x+y=5\)に代入して、\(x=2\)となるので、
林檎は2個で蜜柑は3個となります。
ちなみに林檎という漢字は漢検1級レベルです。
→漢検1級の対策法はこちら
代入法で解く
\(\begin{eqnarray} \left\{ \begin{array}{l} x + y = 5 \\ 50x + 100y = 400 \end{array} \right. \end{eqnarray}\)
上の式から、\(y=5-x\)となるので、下の式に代入する。
\(50x+100(5-x)=400\)になり、整理すると、\(x=2\)となるので、それを\(x+y=5\)に代入して、\(y=3\)となる。
よって、林檎は2個で蜜柑は3個となります。
要はどっちでもOKなのです。もっと慣れたい!って人には次の本をおすすめします!
中学数学を超特急で深く完璧に理解できる良書です!
さて、次に連立方程式の図形的な意味について解説します。ここがメインです。
2元連立1次方程式と1次関数の関係


ここでは、先ほどの問題を可視化して考えましょう!
\(\begin{eqnarray} \left\{ \begin{array}{l} x + y = 5 \\ 50x + 100y = 400 \end{array} \right. \end{eqnarray}\)
これって、よく見ると次のように変形できますよね?
\(\begin{eqnarray} \left\{ \begin{array}{l} y =-x+5 \\ y = -\frac{1}{2}x+4 \end{array} \right. \end{eqnarray}\)
ということは、2式を繋げて次のようにすると・・・
\(5-x=-\frac{1}{2}x+4\)
2直線の\(y\)座標が等しくなる時の\(x\)座標は?という問題ですよね。
では、この2直線を図示して見ましょう!
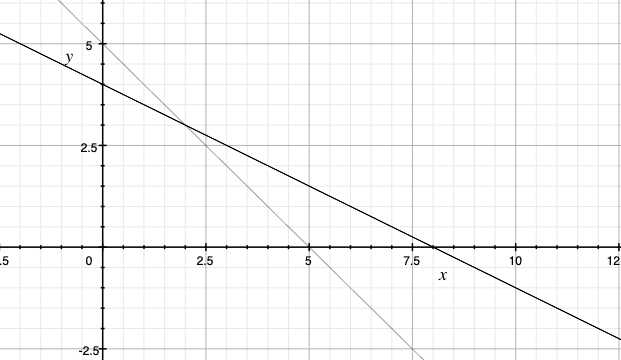
なるほど!交点の座標は、\((x,y)\)=\((2,3)\)ですね。
確かに先ほどの答えと一致しています。



空間内の2直線は次の3つのどれかに分類される!
- 平行である
- 交わる
- ねじれの位置にある

連立不等式まで発展させましょう!
\(\begin{eqnarray} \left\{ \begin{array}{l} x + 2 < 5 \\ -2x + 3 ≥ 4 \end{array} \right. \end{eqnarray}\)
突然ですが、上のような問題を連立不等式と言います。
連立不等式は数直線で考えれば一発!
\(\begin{eqnarray} \left\{ \begin{array}{l} x + 2 < 5 \\ -2x + 3 ≤ 4 \end{array} \right. \end{eqnarray}\)
これを順々に解いていきます。
\(\begin{eqnarray} \left\{ \begin{array}{l} x < 3 \\ -2x ≤ 1 \end{array} \right. \end{eqnarray}\)
\(\begin{eqnarray} \left\{ \begin{array}{l} x < 3 \\ x ≥ -\frac{1}{2} \end{array} \right. \end{eqnarray}\)
よって、3よりも小さくて、\(- \frac{1}{2}\)以上なので、答えは\(- \frac{1}{2}≤x<3\)です。
連立不等式は2つ以上の条件式があっても全く同じで、
- 1つ1つの解の範囲を求めて、
- それらのダブっている部分(共通部分)を考えればOK!
このように、連立方程式から色々な知識や知恵を学べます。
連立不等式が簡単だ!と思ったあなたは受験数学マップを参考に東大レベルまで数学力を伸ばしてください!
お読みいただき、ありがとうございます。


