1次関数と円の方程式は軌跡の求め方を知れば自由自在に求められる！

数検2級の話がメインになりますが、小学生でも高校数学を理解できるようにシリーズ的に書いています。

今回は軌跡の考え方がメインになります。

以前に１次関数は正比例のグラフの発展版であるということは以前に説明しました。

１次関数を勉強したときに勘違いを起こす人がいるんです。

会話相手

何を勘違いするんですか？

数検１級

どんな\(x\)と\(y\)の関係も全て１次関数で表現できる！という思い込みだよ。妄言も甚だしい笑

１次関数は正比例のグラフから発展する最も簡単なタイプなので先に扱ったのです。

もちろん２次関数や３次関数などずっと続きます。

このように関数には色々なタイプがあって、一概に世の中の関係はこれだ！とはすぐには言えません！

それを求めて考えていくのは物理学で、

数学は物理学で立てられた方程式などを解く際に使われている手段であると思っていただけると助かります。

もちろん、数学を研究対象として一生懸命取り組まれている方にとって、

「数学は道具である」という主張は違和感があると思います。

しかし、理系一般の数学の立ち位置と思って聞いていただければ幸いです。

１次関数の決定

１次関数はどのような関数の形だったか覚えていますか？

会話相手

はい！\(y=ax+b\)です。

数検１級

そうだね！では\(a\)や\(b\)を求めるのに、いくつ式があったか覚えてるかな？

会話相手

２つの条件です。\(y\)切片の\(b\)を求める条件と傾き\(a\)を求める条件がありました！

確かにその通りです！以前はそのような問題を扱いました。

そして今回は、より踏み込んだ問題を扱います。

今までの解法と同じように求めると時間がかかります。

会話相手

ここで求める１次関数を\(y=ax+b\)とおくと、私は\(a\)と\(b\)を求めれば良いのですよね？

数検１級

ならば、\(a\)と\(b\)を未知数に持つ連立方程式を作って解けば\(a\)と\(b\)が出るのでおしまいですよね！

求める１次関数を\(y=ax+b\)とおく。

この上を２点\((1,3)\)と\((2,5)\)が通るので、代入すると、

\(\begin{eqnarray} \left\{ \begin{array}{l} a + b = 3 \\ 2a + b = 5 \end{array} \right. \end{eqnarray}\)

この連立方程式を解くと、\(a=2\)と\(b=1\)が得られるので、

答えは\(y=2x+1\)です。

ここで、もっと１次関数を深めて行きましょう。

ここをサボると円の方程式などがわからなくなるからです。

１次関数は何がわかれば決定しますか？

会話相手

傾き\(a\)と\(y\)切片\(b\)ですよね？

数検１級

もうちょっと一般的に答えましょう。

会話相手

あ、なるほど。傾きは絶対に必要ですね。あとは通る１点がわかればOKです！

正解です！

これが分かると面倒な連立方程式を解かずとも一発で１次関数が求められるようになるんです。

では、その公式を出してみましょう！

では導いて見ましょうか。

傾き\(a\)の１次関数を、\(y=ax+b\)とおく。

この上を点\(A(s,t)\)が通るので、\(t=as+b\)が成り立つ。

２つの式を片々引くと、\(y-t=a(x-s)\)が得られる。

これが高２で習う１次関数の公式です。

数検2級レベルです。

では、この公式を使って、次の問題を一瞬で解きましょう。

先ほどの公式を用いると、求める１次関数は\(y-2=3(x-1)\)と表せる。

これを整理して、\(y=3x-1\)となる。

圧倒的楽勝感万歳！

なるほど。１次関数はここまで深められるのですね。

では最後にポイントとしてまとめておきます。

もっと解きたいあなたは次の本がおすすめです。

では、１次関数を無限倍の虫眼鏡で拡大したらどのようになっているのでしょうか？

次はここから扱います。

軌跡の考え方を小学生や中学生が学ぶ意味は大きい！

１次関数\(y=2x+1\)を虫眼鏡で見ると、

これはただの線ではなく無数の点が集まってできた集合です。

この無数の点はある規則に沿って並んでいますが、それはどのような規則か分かりますか？

そうです。

それが\(y=2x+1\)という式（\(x\)と\(y\)の方程式）です。

この考えを一般化して軌跡という考えを導入します。

では、軌跡の定義と考え方をお話しします。

大学入試では軌跡の方程式を求めることが最優先事項なので、出し方を解説します。

1. まず求める点を点\(P(x,y)\)とおく。
2. あとは\(x\)と\(y\)が満たす関係式を全力で求める！
3. その関係式を満たす関数全体が答えなのか？もしくは一部分か?を問題文の条件から吟味する。

最後の一文がわかりにくいと思いますので後ほど具体例を紹介します。

では、軌跡の考えを使って円の方程式を求めましょう！

円の方程式も座標平面上に表現できる！

では質問です！

円ってどうすれば書けますか？

中心を取ってコンパスでぐるっと回せばよいですよね！

小学校でも習う知識ですよね？ではもう少し踏み込みます！

これって先程の１次方程式の決定と同じような考え方ですよね？

では、具体的に円の方程式を導いてみましょう！

さて、この公式を軌跡の考え方を用いて導きます！

まず円上の任意の点を\(P(x,y)\)とおく。

\(P\)がどこにいても常に\(CP=r\)なので、二点間の距離の公式より、

\(\sqrt{(x-a)^2+(y-b)^2}=r\)となる。

この両辺を2乗して、\((x-a)^2+(y-b)^2=r^2\)が得られる。

注意ですが、二点間の距離の公式とは三平方の定理そのものです。

では、最後にいくつかの問題を解いて終わりにしましょう！

ちなみに下に行くほど難しくなりますが、

基本は中心と半径を把握すれば終了ってことだけです。

①番の問題は、公式に代入して\((x-1)^2+(y-2)^2=9\)です。右辺を３にした人はもう一度公式の導き方をご覧ください。

②の問題は、中心が\((0,1)\)なので\(x^2+(y-1)^2=r^2\)まで置けます。

あとはこの上に点\((2,3)\)があるので、\(2^2+(3-1)^2=r^2\)より、\(r^2=8\)が得られるので答えは、\(x^2+(y-1)^2=8\)ですね。

ラストの③は、２点\((1,2)\)、\((3,4)\)を直径の両端に持つので、中心は２点の中点のはずで、中点公式を使うと\((2,3)\)ですね、中心は。

あとは半径ですが、これって２点\((2,3)\)と\((3,4)\)との間の距離なので\(\sqrt{2}\)ですね。

よって答えは、\((x-2)^2+(y-3)^2=2\)ですね。

では最後に本当のラスボスを１題出します！

求める図形は円であるので、上の条件から、\(x^2+y^2=1\)とおける。

加えて下の条件も加味すると、求める図形の方程式は次の条件で表される。

\(\begin{eqnarray} \left\{ \begin{array}{l} x^2+y^2=1 \\ y ≥ 0 \end{array} \right. \end{eqnarray}\)

図は次のようになります。

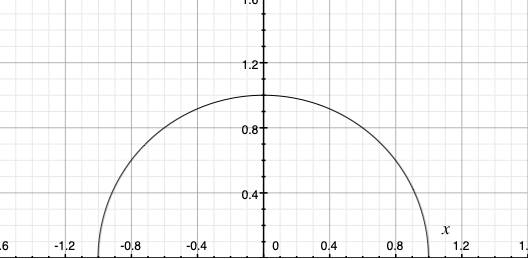
円の方程式は高2で本格的に習います。数検2級レベルです。

円の方程式をもっと解きたい！という人は次も合わせてご覧ください！

お読みいただき、ありがとうございます。