突然ですが、\(-2x+3=-4\)となる\(x\)を求められますか?
算数的な解き方だと\(2x\)を置き換えて・・・とかやりますよね?
それだと計算に時間がかかるのでNGです!
このような問題や、1次不等式の問題などを大学入試の観点から見た時に、
中1にはこのように理解して欲しいな・・・という要望を記事にします。
要望というよりは解き方・考え方なんですがね、教科書に載っていないのでね(汗)
では、今回も本質を伝えることを目標としていきますので頑張ってついてきて下さいね。
移項というテクニックをまずは知ろう!
算数になくて数学にあるものはいっぱいあります。→こちらなど
-

-
文字式計算を3分で理解する方法!文字を使う理由と展開まで教えます
続きを見る
その1つが定義や定理という言葉です。


中1以上の数学では定義を適当に扱っていると大学入試の上級問題とかには手も足も出なくなるのできちんと学習する意欲を持ちましょう。
さて、まずは項と係数と指数について定義を書きます。

\(2x\)や\(x+2\)や\(x^3-1\)などを項という。
そのうち、\(2x\)や\(a^5\)や\(y\)などを単項式といい、
\(x+2\)や\(x^3-1\)などを多項式という。
次に、\(2x\)の2という数字を係数という。
さらに、\(a^5\)の5を指数という。この単項式の係数は1であることに注意!
まずはこの定義を整理しておきました。
次に移項という大事な概念を説明します。



具体例をあげましょう。
\(3=3\)という当たり前の式を書きます笑
じゃあ質問です!左の3(これを左辺と言います)に5を足したら、
=(等号と言います)が成り立つためには、右辺に何を足せば良いでしょうか?
・・・当然5ですよね?
ここら辺は、天秤に3gを両側に乗せているイメージで納得していただくのでOKです。
=ということはつり合っているという意味ですから。
同様に\(3=3\)という式の左辺にどのような数を四則演算しても、右辺にも同じ作業をする必要がありますね。
では、次に難問(初見では)を出しますね。
等式\(3=3\)の左辺の3を右辺に移そうと思います。
これを移項と言います。
左辺の3が消えました。ということは右辺の3から何を引くべきでしょうか?
答えは3です。
でも、いつもこうやって考えていると頭がパンクするので、
次のようなことを覚えて下さい。

移行とは、左辺(右辺でもOK)の値を右辺に移すことですがルールがあります。
\(x=x\)という式があるとします。
- \(a\)という数を左辺に足すと、右辺にも\(a\)を足す必要がある。
- 同様に、\(x-a=x-a\)
- \(ax=ax\)
- 掛け算で成り立つなら割り算でも成立しますよね(0出ないことを要確認!)
これで僕たちは1次方程式を解く準備が整ったんですよ!
理論上、どのような1次方程式もこれで解けます。
1次方程式を1分で出来るようにします
冒頭の問題:\(-2x+3=-4\)となる\(x\)を求めらます。
ちなみにこの上の等式を方程式と言い、等式の文字の指数は大きくても1乗なので1次方程式と言います。
- \(-2x+3=-4\)
- \(-2x+3-3=-4-3\)
- \(-2x=-7\)
- \(x=\frac{7}{2}\)
最後は両辺を−2で割っています。
結構面倒くさいですよね。慣れてきたら移項を頭の中でしましょう!
そうすれば次のように超スピードで解けます。
- \(-2x+3=-4\)
- \(-2x=-7\)
- \(x=\frac{7}{2}\)
はいおしまいです。これだけですよ1次方程式は。
高校入試を控えている人や難しい問題を解きたいあなたには次の本をオススメします。
超難しい本というわけではありませんが、ちょうどいい難易度の難しさのはずです。
正比例の比例って何?1次関数まで教えるよ!
え?次って1次不等式じゃないの?と思ったあなたは教科書の配列に洗脳されていますねw
いいえ。比例を勉強します。
ある特殊な生物がいます。
身長が100cmの時、体重が10kgです。
身長が200cmの時、体重が20kgです。
では、体重が70kgの時、この生物の身長はいくつですか?
このような問題で、小学生は比という考えを使います。
もちろんそれでもOKです。答えは700cmですね。デケェーなーおいw
しかし比の考えには欠点があって、可視化を直接できないという短所があります。
比の考えは原理的で面白いが図に表現するのが難しいのが難点。
だから僕たちは正比例の関数という比を可視化する方法を学ぶのです。
本問では、身長は体重に比例すると考えられる(何倍か?という意味です)ので、
その比例定数(倍率みたいなものです)をまず求めます。
一般に比例定数は文字\(a\)で表現することが多いです。
今回は\(a=10\)ですね。
だから身長を\(y\)で体重を\(x\)とおくと、\(y=10x\)という関係式で表せます。
これを\(y\)は\(x\)の関数であると言います。
今回は、\(y=10x\)の\(x\)が70とわかっているので、代入して\(y=700\)となります。
この解き方、覚えておいて下さい。
数検1級のレベルに飛びますが、微分方程式という分野が出てきます。
そこで比例という概念がわかっていないと解けない問題が出ています。
興味ある人は下記の記事を参照です!
-

-
【数学検定1級】参考書の順番で合格率が上昇(過去問は難易度に注意!)
続きを見る


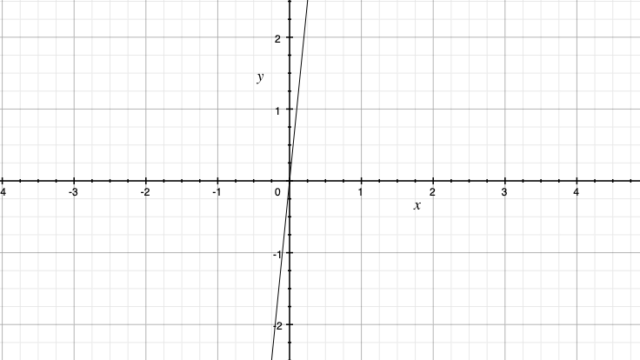
じゃあ次の問題!今度は原点(0,0)を通らないグラフを書いてみましょう。
範囲は数検4級です。
-

-
【数学検定4級】合格率70%で過去問不要?解答が詳しい問題集のおすすめはこれだ!
続きを見る
\(y=2x-1\)のグラフを書いてみましょう。
この2は直線の傾きを表す数字で−1は\(y\)軸と交わる値を表すもので\(y\)切片と呼ばれています。
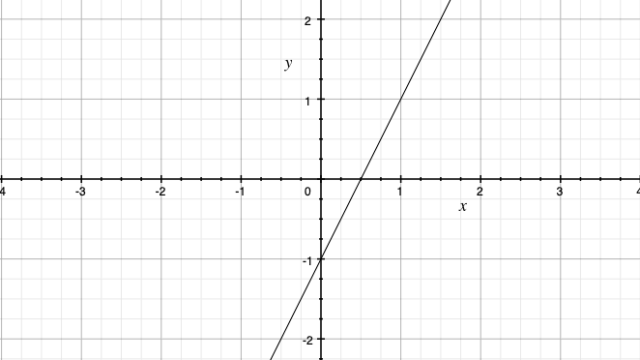
では最後の問題!次のグラフを表す1次関数を求めよ!
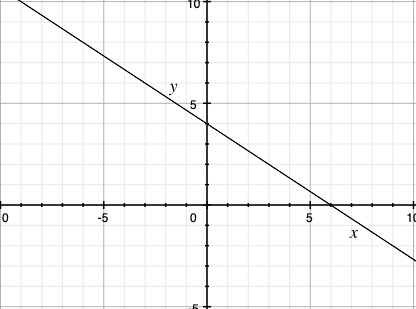
この問題をしっかり考えると、1次関数を一瞬で書けるようになりますので。
答えは\(y=-\frac{2}{3}x+4\)です。
考え方のポイントをまとめておきますね。
1次関数の形は傾きと切片で決まる!
- 傾きとは\(x\)の増加量分の\(y\)の増加量で定義されます。今回は6右に行って4下に下がっている(−4だけ上に上がっている)ので傾きが出ますね。
- 次に切片ですが、これは\(y\)軸と交わっている点を見れば一発です。
式で解く方法もありますが、これは後日の連立方程式のお話で書きますね!
-

-
連立方程式の文章題は解き方の本質ではない!どこで利用するかが大事
続きを見る
ちなみに次の3種類の線にご注意を!

- 直線とはまっすぐに永遠に続く線のことです。
- 線分とは長さが決まっている線のこと。
- 半直線は一方が無限に伸びている線のことです。
中1で習うことですが、今教えておきますよ。
1次不等式は1次関数と一緒に理解するのが効率最高!
質問です!
\(a\gt b\)という式を不等式といい、\(a\)大なり\(b\)と読みますが、どういう意味かわかりますか?
はい。そうです。\(a\)の方が\(b\)より大きいという意味です。
\(a\geq b\)は\(a\)の方が\(b\)より大きいかまたは同じという意味です。
では、不等号の向きが変わる瞬間ってどんな時でしょうか?
例えば両辺にある数を足したり引いたりした場合、向きは変わりますか?
変わらないですよね。
では掛け算はどうでしょう?

不等号の向きが変わる瞬間は次のことをした時だけである。
ちょっと考えれば意味はわかります。
- 両辺に負の数を掛ける時(つまり負の数で割っても変わる)
では、このルールにしたがって、1次不等式を解いていきましょう。
\(3x-2\gt 1\)を解きましょう。不等式は原則では範囲が答えとして出てきます。
- \(3x-2\gt 1\)
- \(3x\gt 3\)
- \(x\gt 1\)
最後は3という正の数で割っているので向きは変わりません。
これでどのような1次不等式も解ける準備ができました。
では、グラフを用いて次の不等式を解きましょう!
\(3x-2\gt 1\)
ここで式の意味を考えるとすぐに解けます。
\(3x-2\gt 1\)をグラフを用いて解くには次の発想の転換が必要である。
\(y=3x-2\)のグラフが\(y=1\)のグラフよりも上にあるような\(x\)の範囲を考えれば良い。
下の図を参考にすると、赤いグラフが青いグラフより上にあるような\(x\)の範囲は、\(x\gt 1\)である。
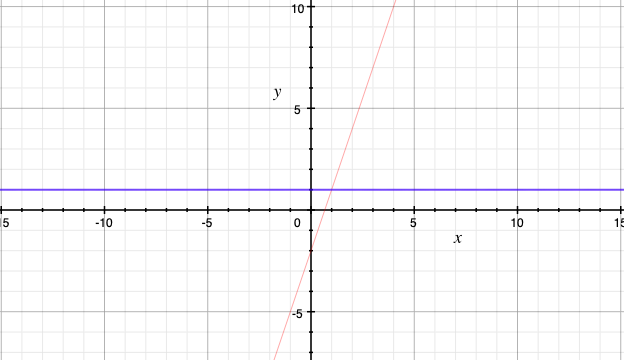
ここまでしっかりと理解できれば高1数学の二次不等式が一瞬で理解できます。
ちなみに数検準2級レベルです。
-

-
【数学検定準2級】過去問解答不要の参考書1冊!高1レベルの難易度で合格率40%問題の対策
続きを見る
反比例の問題も扱います!
さて仲間外れになった反比例の問題を一番最後に説明します。
反比例とは次のような問題設定の問いです。
ある特殊な生物がいます。
身長が10cmの時、体重が10kgです。
身長が20cmの時、体重が5kgです。
では、体重が50kgの時、この生物の身長はいくつですか?
このような身長と体重の積が一定である関係を反比例の関係にあるといいます。
身長を\(y\)で体重を\(x\)とおくと、\(xy=100\)という関係式で表せます。
ただこれでは関数として分かりづらいので、\(y=\frac{100}{x}\)と表現し直して、
これを\(y\)は\(x\)に反比例すると言います。
これをグラフにすると、ちょっと違和感があるかも知れませんが曲線になります。
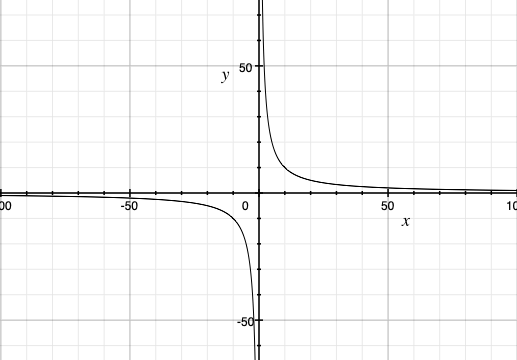
このような曲線を(直角)双曲線といい、\(x\)軸や\(y\)軸を漸近線といいます。
どんどん0に限りなく近づくような振る舞いをしているからですね。
以上です!
この記事をみて、簡単じゃん!ってあなたは数検5級に受かる見込みは十分です!
早速参考書に取り掛かりましょう!
お読みいただき、ありがとうございます。







