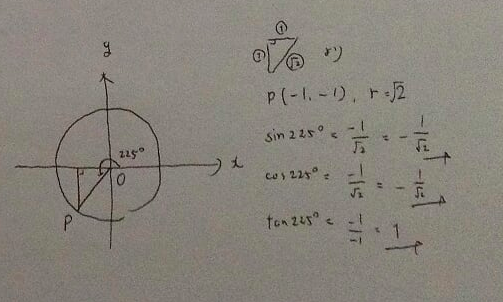サイン・コサイン・タンジェントを1分で教えます

数検１級

サインとかコサインとかってキチンと理解できていますか？

学校などで暗記させられていませんか？

数検2級を目指している方で苦戦される箇所の１つが三角関数です。

今日はそれを一瞬で理解していただくべく記事を書きます。

会話相手

学校の定期試験も大丈夫です！

サイン・コサイン・意味不明！！！

僕が初めて学習した際に心で感じた一句です笑

でもこれって小学生が初めて分数に遭遇した気持ちと似ている筈なんです。小学生で分数は初めての比の概念なわけです。

数検１級

なぜならサインとかコサインって三角形の比のことですからね。

僕たちは比を学習しているんだ！という認識を持っていただく事から学習がスタートします。

始まる前に

サインが正弦、コサインが余弦、タンジェントが正接と習ったと思いますが、

数検１級

なぜ漢字表記がこのようになるのかは多分学校の教員も知らないと思います。

まずはそこから説明します。

正弦

ギリシャの時代に弦という用語ありました。

皆さんご存知の通常の弦という意味合いです。

しかし、インドで「いや、その半分が『まさに正しい弦だ』」という意見が広がりました。

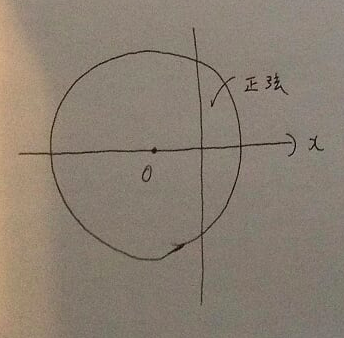
円を座標軸に埋め込んだとき、図のような長さを正弦と名付けたのです。

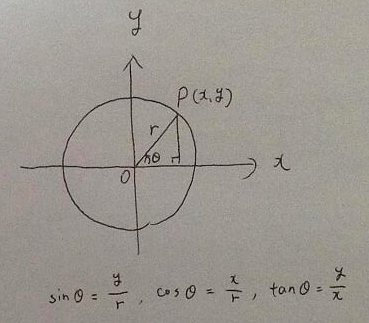
図のように、x軸の正の方向を0°とし、y軸の正の方向を90°に定めるとき、角度θを設定し、直角三角形を作ります。

その時に（円上の点Pのy座標/円の半径）の値をサインθと定義します。

その定義の仕方からサインが正弦と名付けられたのですね。

余弦

直角三角形で直角以外の１つの鋭角をθとすると残りの鋭角は９０°ーθで表せますね。その残りの鋭角を余角と言います。

数検１級

つまり『余角の正弦がコサインの定義』のためコサインを余弦と言います。

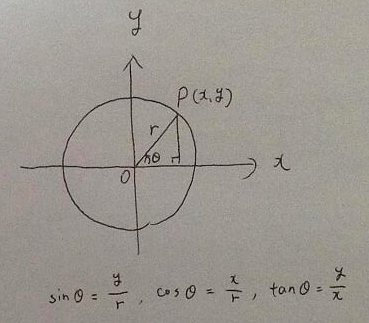
正接

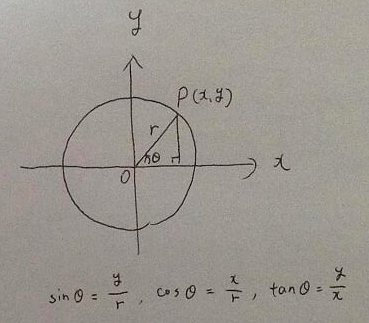
図のようにタンジェントは『直角三角形の辺をx軸に正しく接っすることにより』（Pのy座標/Pのx座標）として定義されるため、

タンジェントのことを正接と言います。

本書も合わせて読むとより理解が深まります。

確認問題

では、本記事のメインです。奮ってご参加ください。

解答は次の記事で書きますね！

お読みいただき、ありがとうございます。