次の問の各集合のうち、どちらの濃度が濃いか答えよ。(3)はその集合の構成を考えよ。
(1)「0から1までの集合」と「0から10までの集合」
(2)「自然数全体の集合」と「実数全体の集合」
(3)「実数全体の集合」よりも濃度が濃い集合を構成せよ。
本記事ではその解答と解説を行います。
復習
無限集合についての記事の復習をオススメします。
数検1級以上の内容ですが、解りやすく書いています。
-

-
頭の体操の問題です!数検1級以上のレベルです
続きを見る
-

-
頭の体操の解答です?数検1級以上のレベルです
続きを見る
さて、準備はよろしいでしょうか?
解答前の準備
解答の前に定義をします
自然数全体の集合の濃度をアレフゼロで定義します。記号は、
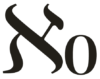
こんな卍(まんじ)っぽい記号です。対して、実数全体の集合の濃度をアレフで定義します。記号は、

これも卍っぽいですが、0が書いていないのが特徴です。
濃度の強さで言うと、アレフゼロ<アレフとなります。
濃度の対等性
集合Aと集合Bの濃度が同じとは1次関数的な対応関係が存在した場合OKです。
本当はもっと複雑ですが本記事では上述のように定義します。
例えば集合Aを整数全体の集合、集合Bを偶数全体の集合とします。
Aの要素をaとすると、2aの値はBの要素になりますね。
つまりAとBの間にはy=2xと言う一次関数的な対応関係が存在するため、集合Bの濃度もアレフゼロとなります。
問題の解答
いよいよ解答です!
ここでもう一度、問題を再び掲載します。
次の問の各集合のうち、どちらの濃度が濃いか答えよ。(3)はその集合の構成を考えよ。
(1)「0から1までの集合」と「0から10までの集合」
(2)「自然数全体の集合」と「実数全体の集合」
(3)「実数全体の集合」よりも濃度が濃い集合を構成せよ。
問題1の答え
同じ濃度でありアレフゼロです。
問題2の答え
実数全体の集合です。自然数全体の集合はアレフゼロで実数全体の集合はアレフゼロであるからです。
問題3の答え
べき集合を考えれば良い。
実際、実数全体の集合Rにおいて、そのべき集合R^Rを考えればその濃度はアレフを超える。
問題3の証明はかなり難しいです。その先を知りたい方は、
などをオススメします。
集合論の深入りは危険?
上に紹介させて頂きました名著についてですが、
初めの本は数学科以外の学部生向きで下の本は純粋数学科向きです。

そもそも集合論自体が抽象的ですので、余程興味がおありの方以外の深入りは危険です。
数検1級チャレンジャーの方は、集合論(の濃度の所は)は範囲外のためオーバーワークです。
つまり数検1級の抽象数学は線型代数の線型空間だけなのかな・・・?
-

-
【数学検定1級】参考書の順番で合格率が上昇(過去問は難易度に注意!)
続きを見る
いずれにせよ、数学の奥の深さが実感できますね。
実際、数学者カントールという方は、アレフゼロ<アレフという命題の証明に命を懸け過ぎて、
精神を病み病院に運ばれてしまった話もあります。

無限はただ大きいだけじゃない!
では、濃度についてまとめましょう。
無限はただ大きいという概念だけでなく、数えられる無限と数えられない無限があり、それぞれの濃度はアレフゼロ、アレフである。
任意の集合の濃度がどうか?については、既知の濃度の集合の要素と未知の濃度の集合の要素との間に1次関数的な対応関係が存在すれば未知の集合の濃度は既知のそれに等しい。
また証明は難しいですが、アレフの先のデカイ無限も無限に作れてしまいます。
頭混乱させてしまった方、すみません。
お読み頂き、ありがとうございます。