反復試行の確率の問題で失敗する確率をかけないとどうなるのか？説明

反復試行の確率でダーっと公式が並ぶわけですが、Cの意味はわかるのに、最後の失敗する確率をかける意味をわからない、

またはかけ忘れる人がたまにいます。

会話相手

それはダメなんですか？

数検１級

数学的にもダメだし、日常生活的にもアウト！

その理由を僕なりに説明します。

反復試行の確率とは？

そして確率は、日本語で「そして」という意味合いを感じたら、どんどん「かけ算」をしていくルールがあります。

その原則にのっとると、反復試行の確率とは次のようになります。

数検１級

n回同じ試行をしてk回成功するとする。成功とは１回成功する確率がpであるものとする。その確率は・・・

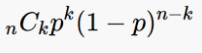
こんな式になります。

初めのCはn回やってk回当たる時の、順番を考えると出てきます。

そして問題は最後の（）で書かれた式です。

もしも最後の（）がなかったら？

会話相手

こんなことですよね笑

数検１級

ではこの式がどんな意味を持っているのかを考えます

上の式に1をn-k回かけても値は変わりませんね。

数検１級

確率1って最強の意味ですよ。1って起こることが100%って意味ですから

つまり上の式って、こんな意味です。

数検１級

n回中k回は成功するよ！そして残りの回数は成功でも失敗でもどっちでもいいよ！

会話相手

なるほど。すごく実際の確率よりも大きな値が出てくるのも納得です

実生活で確率1をかけるということをしてはダメ

こんな面白い本もあるように、基本的に人間って楽観主義の人の方が楽しそうですよね。

しかし、いつでも希望的観測を持っている人って危険です。

それが、成功でも失敗でもどっちでもいいやー！って心境ですよね。

此処一番の生死が決まる勝負で、これをやってしまうとダメですよね。

もっと確率を勉強したいかたはハッと目覚める確率を参照してください。

会話相手

面白いですよ！