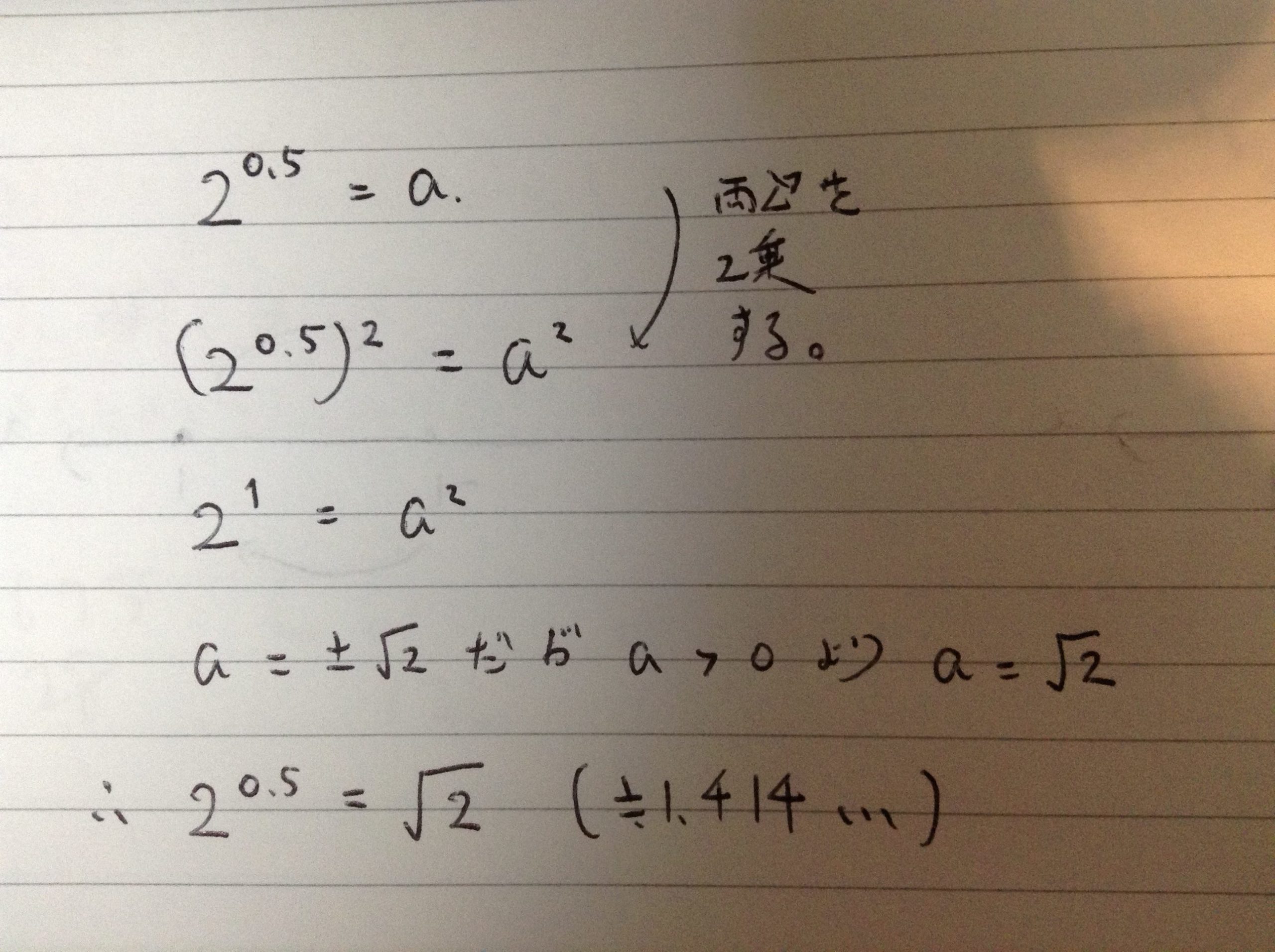これは驚き？！2を0.5回掛け算したら約1.4になります

数検１級

2を0.5回掛けたらいくつになると思いますか？

今日はこのような理屈では解らない問題の解き方を伝授いたします。

記事のレベルは数検2級レベルです。

始まりは小学校１年生

1＋1＝2。

これは、小1で勉強します。

では、2を10回足し算したらいくつでしょう？

1年生は、頑張って足し算をしますが、面倒なことこの上ないです笑

そして掛け算が生まれました。足し算の表記を簡略化するために。

次は九九

小学校では学年が上がるにつれて、算数が苦手な子が増えてきます。

その原因の１つに九九があると思うんです。

九九が出てきた理由は、足し算の簡略化なのですが疑問が生じます。

2×2＝4です。では2を10回掛けたら、どうなりますか？（この答えは1024です。）

これは累乗という話で、中学1年生できちんと勉強しますが、きちんとした値を出すのは求められることは少なく、

どれくらい大きいのか？という桁数を求めさせる問題が高校生では課されます。（数検2級レベル）

例えば、2の100乗は何桁の数ですか？（答えは一瞬で31桁と解りますが、その理由はネタバレになるため数検2級で勉強してください！）

2を0.5回掛けたらいくつになりますか？

本題に移りましょう。

これは考え方がわかれば、かなり面白い教訓になります。

数検１級

その教訓とは「実験」をすることです。

分かる所から順に、未知の領域へと思考して参りましょう。

（このように、人生の困り事でも知っている経験から解決策を推察する、つまり賢者は歴史に学ぶと言う言葉の深さが数学的思考によって正当化されるわけです。）

2を3回掛けると8です。

2を2回掛けると4です。

2を1回掛けると2です。

2を0回掛けると★です。

★は何ですか？

会話相手

ここで規則性を探しましょう。

8→4→2→★

これって2でどんどん割り算していますね！と言うことは、★＝１ですね！

つまり、2を0回掛けると1になるんですね。

？？？

数検１級

頭では受け入れられなくても、理論が語っています、１ですよと。これが数学をやっている面白さの１つです。数学は常識を超える瞬間が多々あります笑

会話相手

では先に進みましょう。

2を3回掛けると8です。

2を2回掛けると4です。

2を1回掛けると2です。

2を0回掛けると1です。

2を-1回掛けると★です。

★って何でしょうか？

会話相手

これも−1回掛けるってイかれてるんじゃないの？！

とツッコミをいただいているとは思いますが、上のルールに則ると0.5ですね。

2をマイナス回掛け算すると、分数が出てきました。

会話相手

では次です。

数検１級

2を0.5回掛け算するとaになります。aはいくつでしょう？

ここで、今までの感覚からaは正の数だとお解りいただけるはずです。

このように両辺を2乗して、指数法則を使っていくのが解答です。

数検１級

実は上で行った2で割っていくという実験も、画像のような方法で行えば直ぐに求めることが可能です。

このようにして累乗の話はどんどん発展していくわけです。

この記事が指数関数につまずいている方の助けに慣れれば幸いです。

お読みいただき、ありがとうございます。