数学的思考力を持つ感覚を体感させます

数検１級

数学検定などを目指されている数学を志す方は、本記事を参考にして頂き学習の指針となされれば嬉しい限りです。

まずは問いかけです

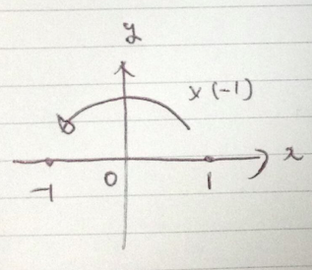
この図を見て下さい。

図のように、ある１点が、１と−１の位置を交互に移動します。

数検１級

では質問です。その点の運動はどのような運動をしていますか？

頭の中で想像をして下さい。

思考の時間です

この時間は至高の時間です。

少なくとも、本問をじっくりと考えると、物の見方が変わってくると思います。ヒントを提示してみました。

自分の答えが絶対合ってる！という方は、下記を読み進めて頂きたく思います。

解答案

ポイント：存在しないを発見する感覚

まずこの問題を多くの方は、まるで点滅する光の点が１と−１を交互に照らすイメージを持たれてのではないでしょうか？

これも１つの答えだと思いますが、この記事は（非常に恐縮ですが）数学力がある状態ではどう見えるのか？

ですので、ふむふむと思って読み進めてやって下さい。

図のように、点が回っていると捉えても間違ってないですよね。

回転の中心は１と−１の中点の０、つまり原点にするのが自然ですね。

つまり下図のようにy軸が見えましたでしょうか？

数検１級

このようにある程度の数学力がある方は、他人が気づかない状況を察知する能力を持っている傾向があります。

ポイント：1を聞いて10を知る

つまり、この運動は点が180度の回転を繰り返している運動な訳ですね。

−１を掛けるということは、点を180度回転させるという図形的性質を持ち合わせているのです。

では欲張ってしましますが（この欲張りの感覚は数学力を上げるためには必要なことです。）90度回転を表す数って一体なんなのでしょうかね？

ここで国語力の出番です。

180度（既知）と90度（未知）の関係性ってどうでしょうか？

それは、90度回転を１回行って、「そして」１回行うと180度になりますね。

このように数学では「そして」という概念を掛け算で表現して行くのです。

確率の独立性などではこの考え使いますよね。←数学検定準2級レベル

つまり180度回転を表す数が、−１ならば、90度回転を表す数をaと置くとa×a=-1

・・・？？？

会話相手

え、こんなaって数ないじゃん！

って思った方、多数のはずです。

ですが、数学は自由な学問です。

確かに、我々の世界（感覚として、この世）にある数の概念ではaは存在しませんが、

数検１級

幻の数（感覚として、あの世の数）虚数を導入すれば存在できます。

数学ではその奥底ではラプラス変換など、

数検１級

違う世界に問題を吹っ飛ばして、そちらで処理して、こっちの世界に持って帰って来る事が往々にあります。

・・・話を数検2級レベルに戻しましょう。

このようなaをiと定義します。

つまり、iを2回掛けると-1になります。つまり、以下の図のような関係が成立します。

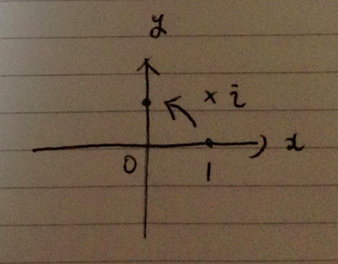
これが、虚数iの正体です。

数学検定2級では、iの意味まで触れませんが、数検準1級になるとここら辺の話がちょろっと出てきます。

虚数が持つ未知の性質に興味がお有りの方は、

異次元の世界での処理法に興味がお有りの方は、

会話相手

共に高校生でも読めるように丁寧に書かれています。レベルは数検１級です。

今の話では、i（を掛ける）が90度回転を表す数であるという結論になりましたが、

これは、−１と１の点の移動から派生し展開して行った訳ですね。

数検１級

つまり数学力がある方は、1つの説明から10（通常は2か3の感覚です）を導ける傾向が強いです。

10をも導ける方はもう数学者なのでしょうね。

数検１級

僕は3程度が多分限界です。

まだまだ沢山面白い例があります！

タイトルのように、皆様の常識を覆すような結果となる問題もあります。

が、それはまた今度の機会に書かせていただきます。

数検１級

数学は独学でやってこそ真の価値があると僕は考えます。

今、学生の方、会社員の方、退職された方、様々な境遇の方がいらっしゃるかと思いますが、

会話相手

知識人の高尚な趣味の１つとして数学のリ・スタートをオススメいたします！

きっと世界（の存在意義）が違って（今までとは変わって）見え、自分の知らない自分に出会えるかも知れません。

それこそ常識を超えて。

お読みいただき、そして問題と向き合っていただき、ありがとうございます。