頭の体操的な問題を出題させていただきました。
-
-
頭の体操の問題です！数検1級以上のレベルです
続きを見る
答えが気になる方もいらっしゃると思うので、解答を書かせていただきます！
まずは問題の復習から
図を見てください！
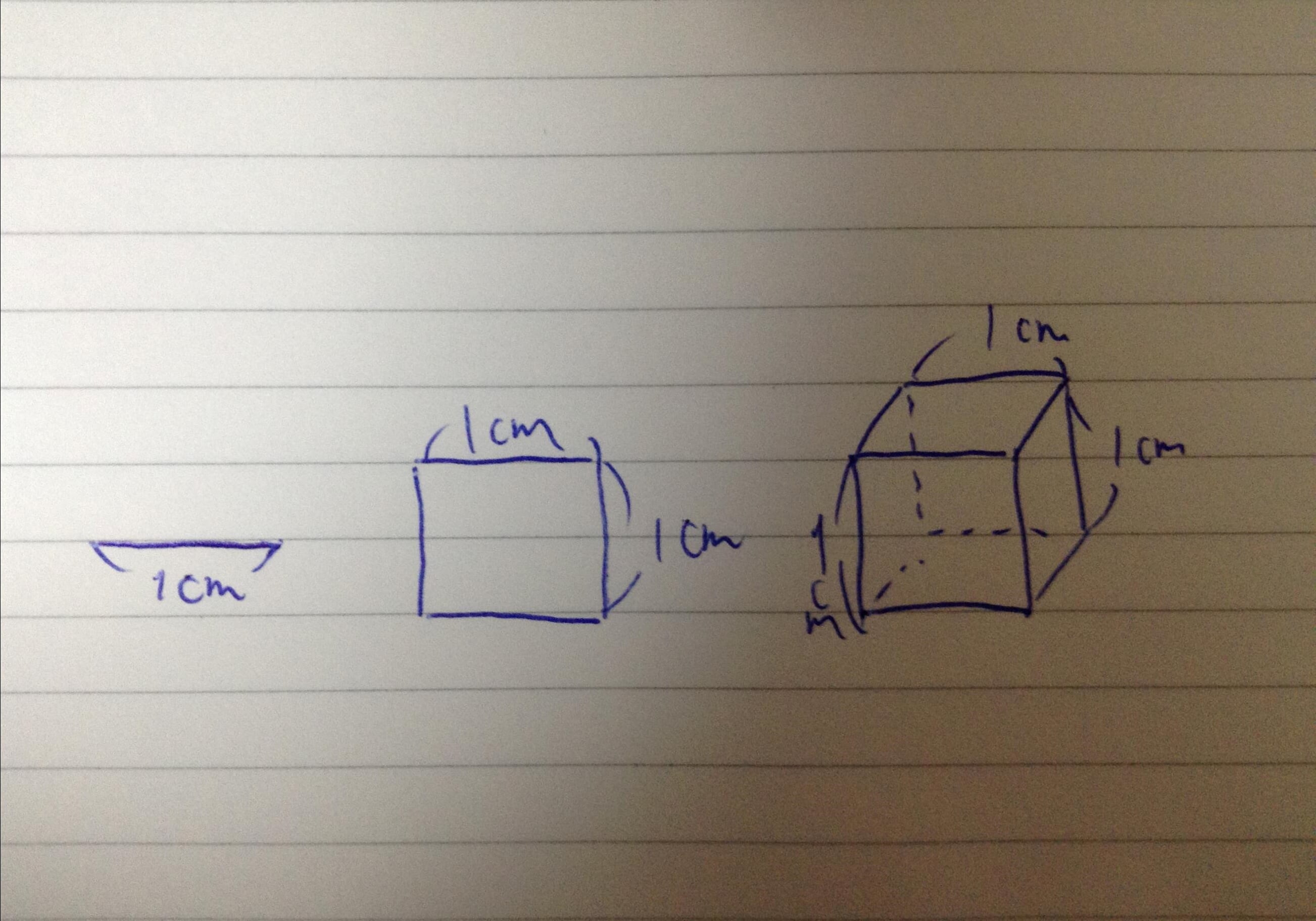
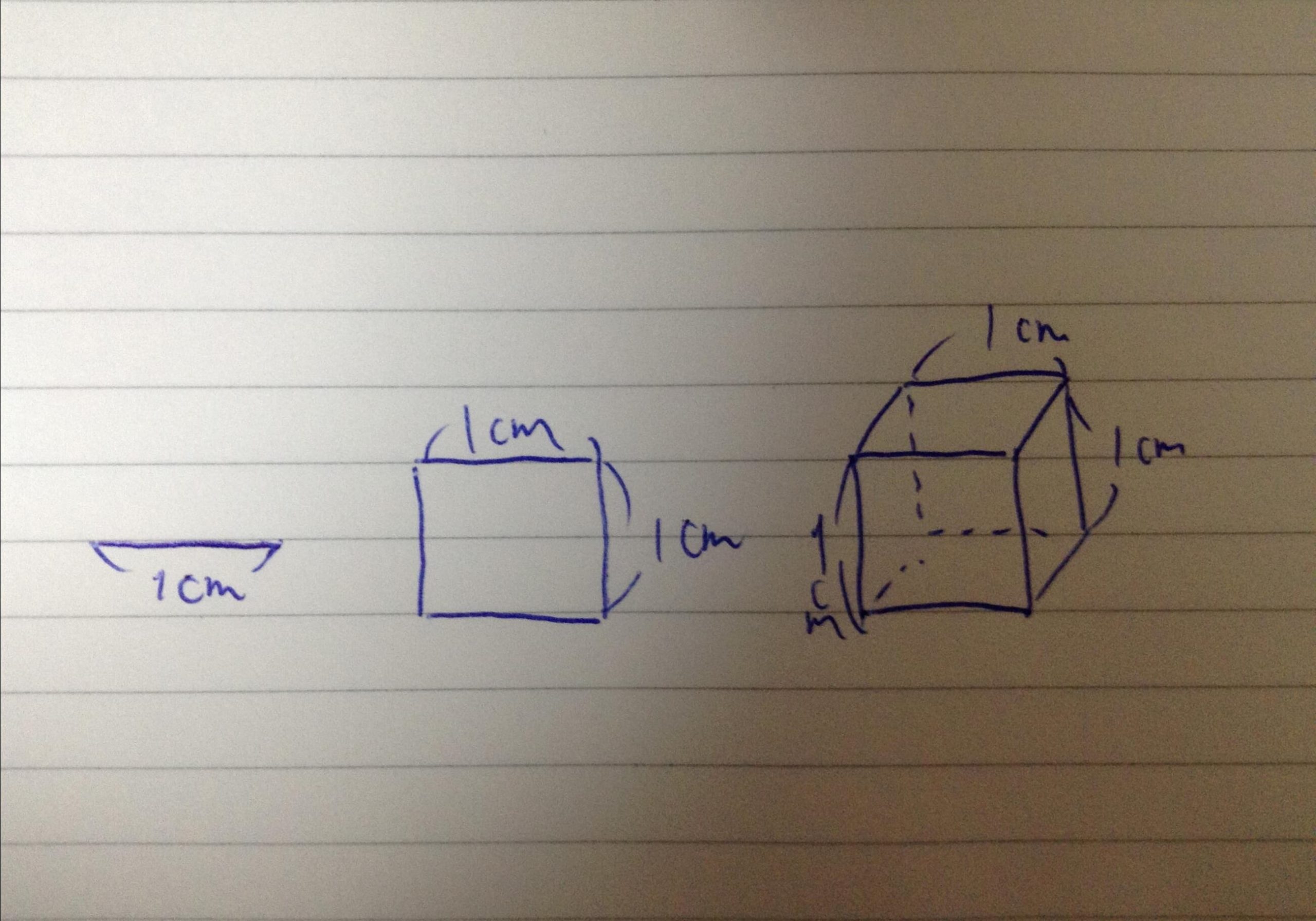
3つの図形がありますよね。
この3つの図形の上から砂粒を落として敷き詰めて行きます。
ただし砂粒の大きさは物凄く小さいものとします。
（１）この３つの図形の中で、最も砂粒が多くなる図形はどれでしょう？
（２）砂粒の数が多い順に図形をお答え下さい。
解答
数検１級
（１）３つとも同じ砂粒です。
会話相手
（２）３つとも同じ砂粒です。
無限集合の不思議
まずは答えを知った方は、えー！！まじかよ！！と驚かれたと思います。
恐らく最初にビックリされたのは数学者カントールだと思います。
なぜなら・・・
無限集合では全体は部分よりも大きいと言う考えが一般に成り立たないからです。
では、疑問になるのは次の問だと思います。では本問の砂粒って何個なの？
アレフ
答えは無限個なのですが厳密にはアレフという記号で表されます。
数検１級
ちなみに4次元の図形でも5次元の図形でも、・・・n次元の図形でも砂粒の個数はアレフとなります。
無限集合の個数に相当する量を濃度と言う言葉で表します。
会話相手
有限集合の個数＝無限集合の濃度と考えていただければOKです。
追加問題
では、追加で理解を深めて行きましょう。
さらに質問です。
解けたらカントールと同じくらい凄い？！
次の問の各集合のうち、どちらの濃度が濃いか答えよ。（３）はその集合の構成を考えよ。
（１）「０から１までの集合」と「０から１０までの集合」
（２）「自然数全体の集合」と「実数全体の集合」
（３）「実数全体の集合」よりも濃度が濃い集合を構成せよ。
（３）は感覚で解けてしまわれたら天才ですね。
僕はこの答えを大学の講義で知った時に数学の底知れぬ深さに戦慄しました。
-
-
無限の上に無限が無限にあります！
続きを見る
お読みいただき、またご考察いただきありがとうございます。
続報をお楽しみに！
