二次関数に入ってから数学が嫌いになった!
という声はいつの時代も聞かれて、困ってしまうものです。
高校数学に入ってから初めに難しく感じてしまう二次関数の全体の理論を、10分で理解していただけるように説明したいと思います。
高校数学〜大学受験数学は教科書や参考書が手元になくても0から解説できますので、
二次関数の章も、教科書とかガン無視で理解重視で行きます!
教科書がわからない!という方には特にオススメです!
二次関数の解き方
二次関数が難しく感じる理由は、中学数学ではドリル的であった数学が、
高校数学では論理体系を帯びてき出すからです。
二次関数は、その論理体系をしっかりと押さえてないと、
きちんとは理解できない分野なので、脱落者が増えるというカラクリです。
二次関数の解き方は基本的には次のような流れになります。
- 二次関数のグラフが書けるようになると、
- 二次関数の問題が解けるようになる。
これが真実です!
では、まず二次関数のグラフを書けるようにしましょう。
二次関数のグラフの書き方
二次関数のグラフを書けるようになれば、
高校数学の二次関数の問題が解けるようになります。
実際、難関大レベルの二次関数の問題もこわくは無くなります。
-

-
大学受験数学の攻略法!教科書からでも最難関までOK
続きを見る
二次関数のグラフを書けるようにするためには、次の流れの理解が必要です。
- 二次関数のグラフを書きたい!
- そのためには平方完成ができるようにならなければダメ!で、
- 平方完成には、理解のための手順があります。
平方完成とは、二次関数の頂点を出すために、必要な式変形です。
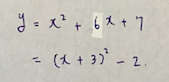
こんな式変形です。
では、平方完成→グラフの流れを具体的な問題を通して説明します。
二次関数のグラフを書く例題
![]()
この二次関数のグラフを書きましょう。
平方完成は、次の3つのポイントで行います。
逆に言えば、その3つのポイントさえおさえれば絶対に解けます。
- 定数項以外を()でくくる
- xの係数に注目して、それを2で割って2乗した数値を使う
- その数値を()中の最後の数字の後に足して引く
係数って何?って人は、次の画像で理解してください。
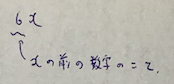
では、式変形を先に載せますね。

ポイントは、3行目の式で9という値を足して引いているところです。
なぜそんな面倒くさいことをするかというと、
その後の式が絶対に因数分解できるからです。
では、最後の式を参考にグラフを書いてみましょう。
最速で理解してグラフを書くためには、次の3つを押さえましょう。
- 頂点はどこか?
- グラフの向きはどっち向きか?
- y軸との交点はきちんと書いたか?
では、説明しましょう。
頂点とは、このようにスヌーピーの鼻みたいなやつです。
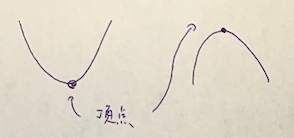
この時にグラフの向きが2つあるのがわかります。
まず、この問題の頂点を図に書きます。
頂点がなんでこの位置かは、
xに具体的な数字を入れて点を書いていくと、確実に分かります。
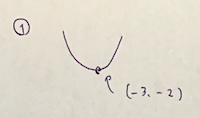
次に、座標軸を書きます。原点Oとx軸とy軸を書かないと減点されるかも。
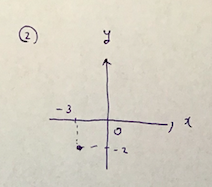
最後に、y軸との交点の情報を書きます。
そしてお終いです。
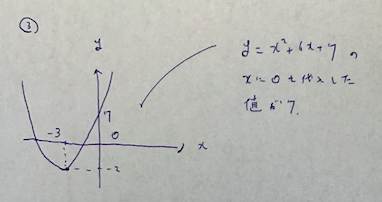
では、次の問題も解いて行きましょう。
![]()
では、次の説明を見ずにできましたでしょうか?

この平方完成から、頂点の座標とy軸の情報を書きましょう。
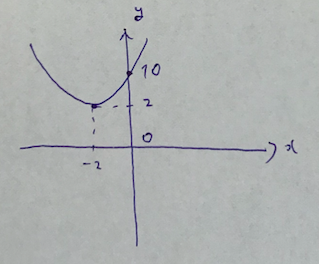
では、最後に皆さんが間違えやすい問題をやってグラフをお終いにしましょう。
![]()
この二次関数のグラフを書きましょう。
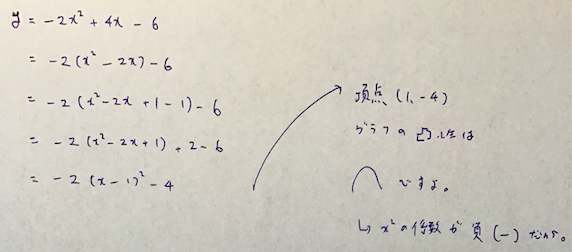
平方完成でミスらなかったですか?
グラフはこうなります。
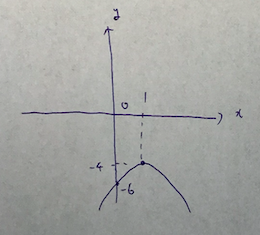
向きがいつもとは逆ですね。気がつきましたか?
二次関数と二次方程式の関係
二次関数と二次方程式の関係を理解しましょう。
平方完成の難しさに比べたら、ここは全く難しくないです。
では、まず次の二次関数のグラフを書きましょう。
![]()
まず展開しますよね!
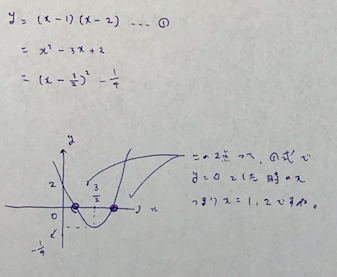
ここで、最後のグラフを見てください。
グラフとx軸との交点って、①式とy=0との交点つまり、
二次関数とx軸の交点になってますよね。
だから、①式を二次方程式と見た時の解なんです!
二次関数とx軸との交点は、
二次方程式の解の値と一致している!
これが真実です。
はい。かなりあっけない真実です笑
しかし、ここからは受験数学向きになりますが、
このあっけない真実を知っていると、グラフが平方完成を経由せずに楽に書けます。
![]()
このグラフを一瞬で書いますね。
まずは、①の二次方程式を解きます。
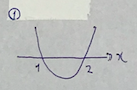
グラフの向きは最高次の係数が+なので、下に凸です。
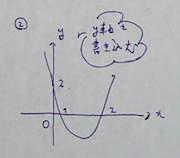
最後にy軸を入れてお終い。
問題文に頂点を求めるとかあったら、ちゃんと平方完成した方が早いです。
しかし、二次関数は対称的なので、
この問題では、1と2の中点が1.5なので、
頂点のx座標が1.5と暗算で出てしまいます。
話題が少し逸れますが、
グラフをx軸方向に〜、y軸方向に〜だけ平行移動しろ!
とか言われたら、頂点を動かせばお終いです。
きちんと考えればわかるので、ここら辺の説明は下記の参考書を見た方が早いです。
独自のメソッドで偏差値を40近く上げた細野さんの二次関数などに特化した理解型参考書です。僕が知る数学の参考書の中で最も軽い重さを誇る参考書です。書き込みスペースが広いため、新品で買った方が本書の利点をよく使えます。
では、二次関数と二次方程式についてもうちょっと踏み込みます。
二次関数の判別式D
二次関数の判別式を意味がわからずに使っている高校生ってめっちゃいると思います。
ここできちんと理解してくださいな。
基本的には、先ほどのポイントがほとんど全てです。
二次関数とx軸との交点は、
二次方程式の解の値と一致している!
では、二次関数とx軸との交点の個数って、

という疑問が沸き起こるのは自然ではないでしょうか?
みなさん思い出してください。
二次方程式って解の公式がありましたよね。
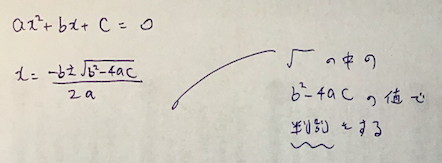
あれのルートの中の中身が+か0かーかで解の個数が違って来ますよね。
その中身をDと表し、判別式と言います。
判別するのは、次の2つですから。
Dの符号で判別できるのは次の2つです。
- 二次関数とx軸との交点の個数
- 二次方程式の解の個数(正確には実数解の個数)
具体的には次の3種類のバージョンがありますが、理解は全然難しくはないです。
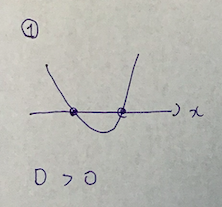
異なる2点で交わる場合ですね。
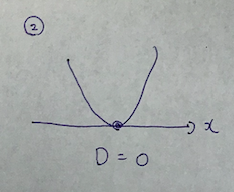
接する場合ですね。
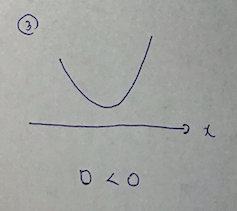
離れている場合ですね。
ちなみに③のパターンは難関大でも問われるので、気をつけましょう。
全ての二次式において、>0が成り立つ場合の〜的な表現の問題で。
では、最後に具体的に練習しましょう。
二次関数の判別式Dの例題
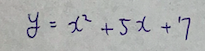
のグラフとx軸との交点の個数を求めよ。
グラフを書いて〜とかはダサいです。


では、最後に多くの高校生が理解不能のまま終わる、
二次不等式の解法の説明をいよいよしていきます。
二次不等式というラスボス
二次不等式とは、一次不等式と違って、感覚的には解けない点が難点です。
だからこそ、二次関数のグラフのイメージがわかないとダメなため、
ここを理解できれば、二次関数の章がほとんど完璧に仕上がっているとみてOKです。
二次不等式は次の3点を踏まえて理解する必要があります。
- グラフとx軸の交点と向きを明確にしてグラフのイメージを書く
- 不等号の向きからグラフとx軸との関係性(上か下か?)を見抜く
- 図を見ながら答えを出す!
教科書にはたくさんの公式が乗っていますが、
上の説明がわかれば公式暗記とはおさらばです。
では、具体的な二次不等式の練習をしましょう。
二次不等式の練習
では、次の二次不等式を解きましょう。
公式なんて知らなくても解けますので、頑張りましょう。
![]()
まずは、上で説明したポイントをしっかりと守る!という意識を持ってください。
- グラフとx軸の交点と向きを明確にしてグラフのイメージを書く
- 不等号の向きからグラフとx軸との関係性(上か下か?)を見抜く
- 図を見ながら答えを出す!
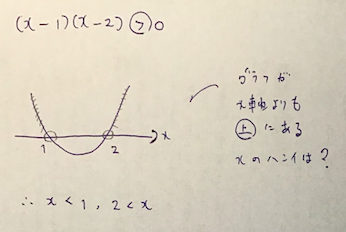
はい。お終いです。
ポイントは、上の図の右側の説明がOKかどうかです。
今は二次不等式ですが、三次不等式以上でも基本的には同じ解法です。
公式なんて覚えてられません。面倒だし。僕はただの暗記は嫌いです。
では、次行きます。
![]()
まずは答えを見ずにトライしましょう!

できましたか?
では、最後にラスボスです。
![]()
制限時間は30秒ですが、できましたか?
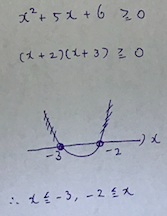
お疲れ様でした!
これで二次関数の全貌を明らかにしました。
二次関数がどのように応用されるか?
二次関数は教科書的な説明は上でお終いですが、
難関大学では、どのように応用されるかを書きますね。
それは通過領域という受験数学最難関分野(整数・通過領域・体積)の1部の、
二次関数を用いた解の存在範囲の問題になります。
二次関数単品では、この応用が最も難しい問題になります。
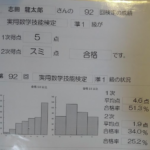
数検で言えば数検準1級クラスですね。
-

-
【数学検定準1級】難易度レベルは受験数学の偏差値帯!合格率を上げる過去問の取り組み方
続きを見る
しかし、今回説明して、皆さんが勉強していただいたお話の内容はちょうど数検準2級のレベルと同等です。
-

-
【数学検定準2級】過去問解答不要の参考書1冊!高1レベルの難易度で合格率40%問題の対策
続きを見る
身につけていただいた知識を、この問題集の過去問を用いて、
アウトプットしていただくのが、よりベストな理解へと繋がります。
皆さんが苦手意識を持ってしまうであろう二次関数の説明に重点をおいた記事を書きました。
お読みいただき、ありがとうございます。