数学で証明がきらい!という人って多いと思います。
僕はその元凶は中学生で習う三角形の合同と相似の証明問題が原因だと思うのです。


本当は覚えることって、ほとんどないのにも関わらずこれでは悪循環です。
そのため、今回は図形の証明に関するコツや具体的な数値計算例を三角形と円に関してお話していきます。


最後に行くにつれて簡単に感じると思いますが、数検対応級は5級~準2級です。
-

-
【数学検定5級】合格率75%!過去問は中学1年生範囲だけど小学生でも合格できるおすすめ問題集を紹介します
続きを見る
-

-
【数学検定準2級】過去問解答不要の参考書1冊!高1レベルの難易度で合格率40%問題の対策
続きを見る
三角形の合同条件
まずは三角形がメインになります。
子供が同じ形の図形を使って遊んでいることがありますね。
例えばこんなおもちゃです。
例えばこの写真にあるような2つの三角形は形が同じなので合同といいます。
ひっくり返したりして2つの三角形が重なれば合同と言えるのです。
中1では、2つの三角形が問題文に書かれてこの2つの三角形は合同であることを証明せよ!と言われます。
数検5級では最も難しい(難しく感じる人が多いという意味です)箇所です。
でも実は覚えることって次の3つしかないのです。
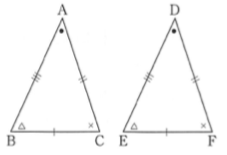
上の図において、\(\triangle ABC \equiv \triangle DEF\)といい、合同であるといいます。
では、どのような時に合同と言えるのか?
それは次の3角形の合同条件の3つのどれかが満たされる時です。(あとで登場する相似条件と混同しないように!)
三角形の合同条件
- 3辺の長さがそれぞれ等しい
- 2辺の長さとその間の角がそれぞれ等しい
- 1辺の長さとその両端の角がそれぞれ等しい
このどれかがOKの時に、三角形同士はピタリと重なることができます。
証明の方法は、次の相似の問題で扱った方が良いと思い、そちらで演習しましょう!
三角形の相似条件と証明のコツ
ドラえもんのスモールライトやビッグライトを当てると、当てられた人ってどうなりますか?
もちろん小さくなったり、大きくなったりしますよね?
これが右手だけが小さくなったけど左足の大きさが変わらないなんてことは起きません。
絶対に、一様に縮小したり拡大したりします。
こういった元の図形とその図形を拡大縮小した図形との関係を相似と言います。
さきほどの合同は相似比が1:1と考えることができますね。


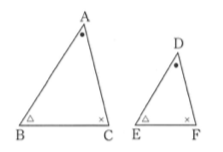
上のような時に\(\triangle ABC \sim \triangle DEF\)と表し、相似であるといいます。
三角形の相似条件
- 2つの角の大きさがそれぞれ等しい
- 2辺の長さの比とその間の角の大きさがそれぞれ等しい
- 3辺の長さの比がそれぞれ等しい
では、いよいよ具体的な問題に挑戦してみましょう。
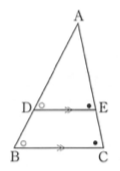
\(\triangle ABC \sim \triangle DEF\)を証明しましょう。
(証明)
\(\triangle ABC \sim \triangle DEF\)を証明する。・・・①
\(\triangle ABC \)と\(\triangle DEF \)において、
同位角より、\(\angle ADE\)=\(\angle ABC\)・・・②
同位角より、\(\angle AED\)=\(\angle ACB\)・・・③
よって、②と③より、2つの角の大きさがそれぞれ等しいので、
①は証明された。(証明終わり)
このように書けばOKです。以下、減点ポイントです!
- 「それぞれ」を書かないとNG!
- 対応する角度の順番がめちゃくちゃは最悪!
では、有名の問題を解いてみましょう!
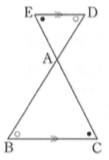
\(\triangle ABC \sim \triangle ADE\)を証明しましょう。
(証明)
\(\triangle ABC \sim \triangle ADE\)を証明する。・・・①
\(\triangle ABC \)と\(\triangle ADE \)において、
錯角より、\(\angle ABC\)=\(\angle ADE\)・・・②
錯角より、\(\angle ACB\)=\(\angle AED\)・・・③
よって、②と③より、2つの角の大きさがそれぞれ等しいので、
①は証明された。(証明終わり)
もちろん対頂角に注目してもOKですよ!
相似は中2で学ぶ内容なので、数検4級の範囲になります。
-

-
【数学検定4級】合格率70%で過去問不要?解答が詳しい問題集のおすすめはこれだ!
続きを見る
おすすめはこの問題集です。
高校入試のことを考えると、『レベルアップ演習』がお手頃だと思います。
もっと難しい問題を解きたい人は『日々のハイレベル演習』という最高ランクの本があります。
大学入試のみを見据えている人はこの本までは不要です。
数学の完全マップに従って、大学入試数学のクリアを目標に頑張ってください。
-

-
大学受験数学の攻略法!教科書からでも最難関までOK
続きを見る
三平方定理は計算ができればOK!
三平方の定理は中3の内容(数検3級)ですが、
さきほどの合同や相似の問題とは違って、大学入試でも頻繁に使われることが多い定理です。
-

-
【数学検定3級】合格率60%のレベルの難易度で過去問不要!合格点を取るために必要な参考書や問題集を解説
続きを見る


では、まずこの有名な三平方の定理を紹介します。
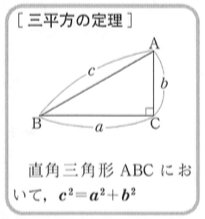
とてもシンプルな定理ですよね!


では、この美しい定理の有名な証明を紹介します。
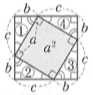
多分最も有名な証明だと思うので、こちらで紹介します。
もうこの図の全てがヒントのようなものですが笑
(証明)
\(b^2+c^2=a^2\)を証明する。・・・①
上の図のように正方形を作る。
中央部の正方形の面積を全体の正方形から4つの直角三角形を引いて求めることを考える。
中央部の正方形の面積は、\(a^2\)・・・②
同様にこの値は、\((b+c)^2- 4\times \frac{1}{2} bc\)・・・③
③を整理すると\(b^2+c^2\)となり、これは②と等しい。
よって、①は証明された。(証明終わり)

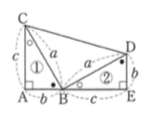

では、具体的な問題を解いてみましょう。
実際の大学入試などでは三平方の定理は計算がメインであるからです。
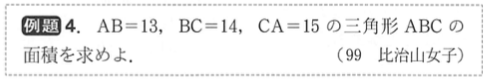
この問題は『スタートダッシュ中学数学』から抜粋しました。本書はめっちゃおすすめ!
解答は次の通りです。
ポイントは未知数を導入していくことです!
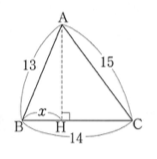
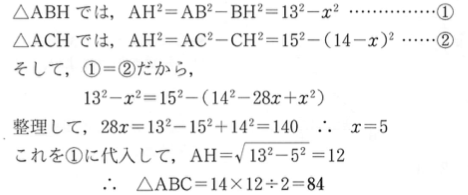
三平方の定理の本格的な問題では、方程式を立式する必要性が出てくる!
円周角の定理が円の性質で最も重要な定理です!
先程までは三角形の問題ばかりだったので、最後に円のお話になります。
レベルは高1(数検準2級)です。
学年は上がるのですが、さきほどと違って証明がほとんど出ませんw
しかも問題の多くは、角度や長さを求めよ!でおしまいなので、
ちょっと勉強すれば点数が取れるお買い得な分野です。


しかし理解をするためには円特有の用語を覚える必要があります。
まずは下の図で円周角と中心角を覚えて下さい。
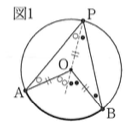
\(\angle AOB\)を弧ABに対する中心角といい、
\(\angle APB\)を弧ABに対する円周角という。
そして下の図で弦という用語を覚えてください。ちなみに弧も。
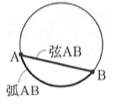
では、準備ができたので順に2つの定理を紹介します。

具体的な問題は次のような問題です!
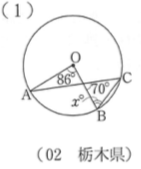
さて、求められますか?

他のタイプの問題や見抜きぬくい問題などはセンター試験にも出ます。
基本的な問題は数検準2級の参考書で、
見抜きにくいタイプの問題は1対1対応の演習で演習をしていただけると嬉しいです。
三角形においてはまだまだ、そこそこ?の定理が残っています。
しかし中学生ならばこの程度の内容を理解していれば高校入試で難関校を目指さない限りはOKです。
高校入試で最難関校を目指すあなたは是非とも日々のハイレベル演習をみっちり頑張ってください。
かなり偏差値が一気に伸びるはずです。
お読みいただき、ありがとうございます。







