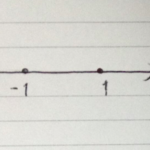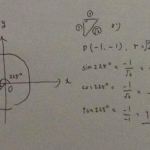複素数の受験問題を解く鍵は3つの見方を使い分けることだった！

数と聞かれて、あなたはどのような数字を思い浮かべますか？

１や\(\frac{1}{3}\)や－9などもあり得ますね。

人によっては\(\pi\)やeなどを例に出してくれるかも知れません。

実は、そのような数のことを実数というのです。

この実という漢字はどのような意味か分かりますか？

そうです。リアルという意味です。

リアルに、そして感覚的に、確かに存在する数のことです。

では、虚数とはどういった数か分かりますか？

この世に存在しない数？？

まぁそのような意味合いでしょうね。

• どういった数が虚数というのか？
• 虚数はどのように数学的に使われているのか？を説明していきます。

ちなみに実数と虚数を合わせて複素数といい、

受験数学では数と言ったら特に指定のない限りは複素数と考えてください。

複素数は大学入試では3つの性質を使いこなせればOK

複素数の世界はとても広く、大学数学では複素関数という分野もあるほどです。

参考（数検１級範囲です。）オススメ参考書はこちらです。

注意：現在、改訂版が出版されています。僕が東大院試で使用したバージョンを載せます。

受験数学では、この広い広い複素数の特徴のうち、

3つだけを使いこなせればOKということを、まずは把握してくださいね。

では、順に考えていきましょう。

複素数の代数的性質

2乗して負の数になる数を虚数といいます。

例をいくつか紹介します。

これは、\(x=±2i\)ですね！

次に、\(i\)が入った四則演算をしましょう。

これも順に解いていきましょうか。

\(-i\)と\(-3\)ですよね、はじめの２問は。

会話相手

最後の商について、これって分母の有理化みたいな設定でしょうかね？

数検１級

その通り！分母には算数的に自然な数を入れるので、虚数が分母ではアウトなのですよ。つまり、分母を実数化する必要が出てくるよ。

つまり分母と分子に\(i\)をかけると分母が実数になり、

答えは\(\frac{i-1}{-1}\)=\(1-i\)ですね。

これに関する問題の類題などは、モノグラフの問題が面白い問題が多いので、是非ともご参考になさってください。

複素数の和と差についての性質

先ほどは複素数を自然な形で演算を取り入れてみました。

ここでは、その妥当性について考えます。

まずは、複素数は\(i\)についての恒等式と見ることもできる！という事実を確認しましょう。

例えば、次のような問題を解けますか？

これも素直に考えてください。

両辺がイコールと言うことは、\(a=3\)と\(b=4\)しかあり得ないですよね。

このような問題は複素数の相当という概念から生まれます。

会話相手

相当ってなんですか？

数検１級

ある数などに四則演算を定義したければ（今回は複素数）、イコールが成り立つときの条件を定義する必要があるんだ。これは主に大学数学で大事になるけど、高校数学でもベクトルなどでも学習した内容なはずだよ。

ここで皆さんベクトルを思い出して下さい。

ベクトルも結局は文字式のように扱って良かったんですよね。

もちろん例外はありますが、和と差に関してはOKですよね。

複素数も同様です。

では、準備が整ったので、複素数の和と差について定義します。

差も同様です。

つまり、複素数同士の和と差はベクトル的性質を持つのです。

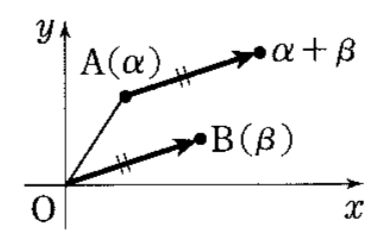
あなたは、この図的な理解ができればOKです。

なぜかと言いますと、この部分が複素数の和と差の本質であるからです。

何も説明をしていませんが、この\(α\)と\(β\)は複素数で、実部と虚部を座標平面上に置いています。

そのためには座標平面上で複素数を埋め込むという作業が大事です。

このようにして複素数を埋め込んだ座標平面のことを複素数平面といいます。

以下の図を複素数平面の定義としてとらえていただきたいです！

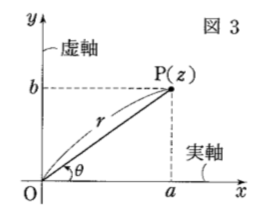
以上で、複素数の和と差の演算がベクトルの和と差の演算に対応していることが分かりましたね。

このように、まずは複素数を図的に見る癖をつけましょう。

この類題はやはり『１対１対応の演習』がベストでしょう！

複素数の関数的性質つまり回転的な性質は積と商で表れる！

まずは次の図をご覧ください！

何を意味しているかお分かりでしょうか？

つまり、−１を掛けるという意味はどのような図形的な意味を持つのでしょうか？

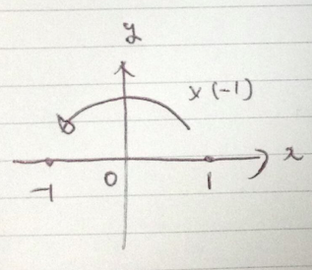
−１を掛けるというのは、180度回転という意味合いを持ちます。

より正確に言いますと、180度回転をさせる関数的な作用を意味します。

では、\(i\)を掛けるというのは、どのような意味を持つのでしょうか？

結論は、90度回転をさせる関数的な作用を意味します。

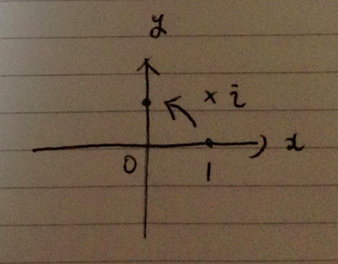
より詳しくは次の記事をご覧ください！

では、この考えを一般化する前に、極形式という複素数の第2の表現法を教えます！

この図からもお分かりのように、

複素数を適当に１つ与えると、原点（極）からの距離（絶対値）と

\(x\)軸（実軸）との成す角（偏角）（範囲は0°～360°）で一意に書けますよね？

三角関数の定義を思い出していただけると、お分かりいただけるはずです。

では、まとめます。

この説明は大学への数学の増刊号より抜粋させていただきました。

では、複素数の積についていよいよ解説します。

まず普通に計算すると、積は2です。

では図的な振る舞いを考えましょう。

それぞれの複素数の絶対値はどちらも\(\sqrt2\)ですね。

偏角はそれぞれ、45°と315°です。

ここで、絶対値をそれぞれかけると2で、偏角を足すと360°ですよね？

その結果を表す複素数って実軸の2の位置にいませんか？

大事なのは絶対値どうしはかけ算で、偏角同士は足し算という結果になることです。

どんな問題でも絶対にこのようになります。

証明は加法定理で一発です。

このように複素数と図形との絡みにまで、本記事の内容を適用できれば入試はOKです。

具体的な問題は、やはり『１対１対応の演習』の数問でテンプレート問題を把握して、吸収してくださいね。

１つ受験問題を紹介しますと、複素数を使いこなせると、このような問題も解けてしまいます。結構面白いですよね！

ポイントは、どんな複素数を与えても、その数には絶対値を何倍して偏角をどれくらい動かせ！と言う命令的な意味（関数的意味）を含んでいると言う事実です！

ぶっちゃけると、複素数はこの事実が分かってしまうと、後は演習をこなすだけです。

お読みいただき、ありがとうございます。